9.0
general documentation
Loading...
Searching...
No Matches
How to use CDO/HHO schemes

Introduction

Compatible Discrete Operator (CDO) and Hybrid High-Order (HHO) schemes are available in code_saturne as alternative space discretizations to the legacy Finite Volumes (FV) schemes. These are new generation of space discretizations dedicated to polyhedral meshes. The capabilities of these schemes in terms of physical modelling are limited compared to the legacy FV schemes.

Overview

With CDO schemes, the resolution of the following models/equations are available:

  • User-defined scalar-valued or vector-valued equations with
    • unsteady term
    • advection term (the advection-field can be user-defined or one retrieves the mass flux from the Navier–Stokes equations or the Darcy velocity from the Richards equation for instance)
    • diffusion term with a homogeneous or heterogeneous + isotropic/orthotropic or anisotropic diffusivity tensor
    • reaction term (also called implicit source term in the FV parts of this documentation)
    • source terms (also called explicit source term in the FV parts of this documentation)
  • Steady/unsteady Stokes or Navier–Stokes equations in a laminar flow regime : NavSto module
    • Several velocity/pressure coupling algorithms are available: monolithic, artifical compressibility or prediction/correction algorithm
    • Please refer to the dedicated page for more details.
  • Thermal systems with the possibility to model phase-change (liquid/solid)
  • Groundwater flows: GWF module
    • This module computes the Darcy velocity from the hydraulic state of the soil seen as porous media and can advect tracers (possibly radioactive tracers) in that soil.
    • Please refer to the dedicated page for more details
  • Solidification process:
    • This module relies on the NavSto module and the Thermal module. Phase transitions between solid and liquid states (solidification or melting) are taken into account.
    • Segregation phenomena can be considered with binary alloys
    • Please refer to the dedicated page for more details
  • Wall distance computations.
  • Maxwell module. This is an on-going work. Up to now, electro-static and magneto-static problems are available.

Moreover, it is possible to setup advanced SLES (Sparse Linear Equation Solver) settings. More details are available here

To get started

A simple example relying on the resolution of the Laplace equation (steady isotropic diffusion equation with Dirichlet boundary conditions) in a cube with CDO schemes is available here. This is a good starting point for beginers.

Case settings for CDO/HHO schemes

To set-up a CDO computation, one has to update the cs_user_parameters.c file and edit successively the following functions

In addition, volume or boundary zones useful to set properties, equations, etc. are defined either thanks to the GUI or by editing the function cs_user_zones for more advanced definitions from the file cs_user_zones.c. This is similar to what is done with the legacy FV schemes.

More precisely, in each function above-mentioned the following settings can be done:

  • cs_user_model
    • Activation of CDO/HHO schemes,
    • Definition of the domain boundaries
    • Add new user-defined equations
    • Add new user-defined advection fields
    • Add new user-defined properties
    • Activate predefined modules (GWF, solidification, Navier–Stokes, thermal system or wall-distance computation)
  • cs_user_parameters
    • Definition of the time stepping strategy (if different from the one pre-defined in th GUI)
    • Definition of the logging/restart frequency
    • Update of the numerical settings of each equation thanks to cs_equation_param_set (including the way to solve the linear or the non-linear equations).
  • cs_user_finalize_setup
    • Complete the definition of advection fields
    • Complete the definition of properties.
    • Complete the definition of an equation
      • Definition of boundary conditions
      • Definition of initial conditions
      • Defintion of source terms,
      • Activate predefined terms of a user-defined equation
        • The unsteady term by adding a link between an equation to a property
        • The advection term by adding a link to an advection field
        • The diffusion term by adding a link to a property
        • The reaction term by adding a link to a property

Settings done in cs_user_model()

Activation of the CDO/HHO part

The very first step is to activate the CDO module in the function cs_user_model There are two ways to switch on CDO/HHO schemes:

  • CS_PARAM_CDO_MODE_ONLY for a usage of CDO or HHO in stand-lone (i.e. without the legacy Finite Volume approach)
  • CS_PARAM_CDO_MODE_WITH_FV for a usage which can share some equations/models solved with CDO/HHO schemes and some other equations/models solved with the legacy Finite Volume approach.

CDO/HHO schemes can be activated within this function as follows:

{
cs_param_cdo_mode_set(CS_PARAM_CDO_MODE_ONLY);
}

Domain boundaries

Domain boundaries are useful for the (Navier-)Stokes equations or for the computation of the wall distance. Several types of domain boundaries can be defined. They are gathered in cs_boundary_type_t (a flag built from a set of predefined bits)

The definition of the domain boundaries for CDO/HHO schemes is performed in two steps: (1) set the default boundary and then add other boundaries which do not fit the default one. The two possible default domain boundaries are CS_BOUNDARY_WALL or CS_BOUNDARY_SYMMETRY Here is a first example.

{
cs_domain_t *domain = cs_glob_domain;
cs_boundary_t *bdy = domain->boundaries;
/* Choose a boundary by default */
cs_boundary_set_default(bdy, CS_BOUNDARY_WALL);
/* Add a new boundary
* >> cs_domain_add_boundary(boundary, type_of_boundary, zone_name);
*
* zone_name is either a predefined one or user-defined one
* type_of_boundary is one of the following keywords:
* CS_BOUNDARY_WALL,
* CS_BOUNDARY_INLET,
* CS_BOUNDARY_OUTLET,
* CS_BOUNDARY_SYMMETRY
*/
cs_boundary_add(bdy, CS_BOUNDARY_SYMMETRY, "sym");
}

Here is a second example.

{
cs_domain_t *domain = cs_glob_domain;
cs_boundary_set_default(domain->boundaries, CS_BOUNDARY_WALL);
/* Define an "inlet" boundary */
cs_boundary_add(domain->boundaries,
CS_BOUNDARY_INLET | CS_BOUNDARY_IMPOSED_VEL,
"inlet_faces"); /* boundary zone name */
/* Define an "outlet" boundary */
cs_boundary_add(domain->boundaries,
CS_BOUNDARY_OUTLET,
"outlet_faces"); /* boundary zone name */
}

Activate predefined equations

Several predefined models are available (and thus equation or set of equations). When activating a predefined module, this implies:

  • adding equations and variable fields;
  • adding properties (and sometimes an advection field);
  • adapting the default numerical settings of the added equations to get more relevant settings.

Navier-Stokes (NavSto module)

Please refer to the dedicated documentation available here.

Groundwater flows (GWF)

Please refer to the dedicated documentation available here.

Solidification/melting module

Please refer to the dedicated documentation available here.

Thermal system

The activation of the thermal module yields the following actions:

  • Add an equation called "thermal_equation" (the name of the associated variable depends on the choice of the variable, by default, the variable is "temperature")
  • Add the properties "mass_density", "thermal_capacity" and "thermal_conductivity"

For the thermal equation, the default boundary condition is a no flux (i.e. a homogeneous Neumann boundary condition). Here is the simplest example to activate the thermal module.

{
cs_thermal_system_activate(0, /* model flag (0=default) */
0, /* numeric flag (0=default) */
0); /* post flag (0=no automatic post-process) */
}

The first parameter is a flag to describe the thermal model to consider. This flag can be built from the following tags (cs_thermal_model_type_bit_t)

To specify the choice of the variable used in the thermal model (by default, the temperature in Kelvin). This can be modified by adding the tag

and to change the main variable use the one of the following tag

The two previous options are not fully implemented.

The second parameter is a flag related to the numerical aspects. There is no tag available up to now.

The third parameter is a flag related to the activation of automatic post-processings.

Wall-distance computation

It is possible to activate the computation of the distance to the wall using CDO schemes (CDO vertex-based schemes are used) as follows:

{
/* Activate predefined module as the computation of the wall distance */
cs_walldistance_activate();
}

Add a property

User-defined properties are added thanks to a call to the function cs_property_add in cs_user_model Here are several examples:

{
/* For an anistropic property (tensor-valued) */
cs_property_add("conductivity", /* property name */
CS_PROPERTY_ANISO); /* type of material property */
/* For an isotropic property (scalar-valued) */
cs_property_add("rho.cp", /* property name */
CS_PROPERTY_ISO); /* type of material property */
}

The function cs_property_add returns a pointer to a cs_property_t structure which can be used to set advanced parameters. If the pointer to a cs_property_t structure is not available, this can be easily recover thanks to a call to the function cs_property_by_name

To enable the computation of the Fourier number related to a given property in an unsteady simulation proceed as follows:

{
/* Retrieve a property named "conductivity" */
cs_property_t *pty = cs_property_by_name("conductivity");
/* Activate the computation of the Fourier number for this property */
cs_property_set_option(pty, CS_PTYKEY_POST_FOURIER);
}

Add an advection field

The definition of an advection field allows one to handle flows with a frozen velocity field or the transport of scalar quantities without solving the Navier-Stokes system. The add of a new user-defined advection field with CDO/HHO schemes is specified as follows:

{
/* Add a user-defined advection field named "adv_field" */
cs_adv_field_t *adv = cs_advection_field_add_user("adv_field");
assert(adv != nullptr);
}

When an advection field is defined, it is possible to retrieve it and then set a post-processing operation. For instance, to activate the post-processing of the CFL number proceed as follows:

{
/* Retrieve an advection field named "adv_field" */
cs_adv_field_t *adv = cs_advection_field_by_name("adv_field");
/* Compute the Courant number (if unsteady simulation) */
cs_advection_field_set_postprocess(adv, CS_ADVECTION_FIELD_POST_COURANT);
}

Add a user-defined equation

User-defined equation with CDO/HHO schemes are added thanks to a call to the function cs_equation_add_user in cs_user_model Here are several examples:

{
cs_equation_add_user("my_equation", /* name of the equation */
"my_variable", /* name of the associated variable */
1, /* dimension of the variable */
CS_BC_SYMMETRY); /* default BC */
/* Add a new user equation.
* The default boundary condition has to be chosen among:
* CS_BC_HMG_DIRICHLET
* CS_BC_SYMMETRY
*/
cs_equation_add_user("AdvDiff.Upw", // equation name
"Pot.Upw", // associated variable field name
1, // dimension of the unknown
CS_BC_HMG_DIRICHLET); // default boundary
cs_equation_add_user("AdvDiff.SG", // equation name
"Pot.SG", // associated variable field name
1, // dimension of the unknown
CS_BC_HMG_DIRICHLET); // default boundary
}

There is an other way to add a user-defined equation relying on the function cs_equation_add_user_tracer which combines (1) the add of a user-defined equation and (2) its association with properties for the unsteady and/or the diffusion term along with the association with an advection field.

{
/* Add the user-defined advection field */
cs_adv_field_t *adv_field = cs_advection_field_add_user("adv_field");
/* Add the user-defined diffusion property */
cs_property_t *diff_pty = cs_property_add("diff_pty", CS_PROPERTY_ISO);
/* Add the user-defined time property */
cs_property_t *time_pty = cs_property_add("time_pty", CS_PROPERTY_ISO);
/* Add a new user-defined equation and associate this equation with some
properties to get a scalar-valued unsteady convection/diffusion
equation */
cs_equation_add_user_tracer("MyTracerEq", /* Eq. name */
"MyTracerVar", /* Variable name */
1, /* Variable dim. */
CS_BC_SYMMETRY,
time_pty,
adv_field,
diff_pty);
}

Settings done in cs_user_finalize_setup()

Boundary conditions

User-defined equations

{
cs_equation_param_t *eqp = cs_equation_param_by_name("AdvDiff.Upw");
cs_equation_add_bc_by_analytic(eqp,
CS_BC_DIRICHLET,
"boundary_faces", // zone name
_define_bcs, // pointer to the function
nullptr); // input structure
}

Thermal system

The mechanism is the same as for user-defined equations. The name of the equation is defined in the macro CS_THERMAL_EQNAME

{
/* Define the boundary conditions */
/* ------------------------------ */
cs_equation_param_t *eqp = cs_equation_param_by_name(CS_THERMAL_EQNAME);
double Tleft = -1; /* Dirichlet BC value */
cs_equation_add_bc_by_value(eqp,
CS_BC_DIRICHLET,
"left",
&Tleft);
double WallFlux = 2; /* Neumann BC value */
cs_equation_add_bc_by_value(eqp,
CS_BC_NEUMANN,
"wall",
&WallFlux);
/* Robin BC values are defined such that:
* normal_flux = alpha * (T - T0) + phi0 */
double RobinBCs[3] = {10, /* alpha */
1, /* T0 */
-2}; /* phi0 */
cs_equation_add_bc_by_value(eqp,
CS_BC_ROBIN,
"right",
RobinBCs);
/* The remaining part of the boundary faces are set to a homogeneous Neumann
BCs (the default BC) */
}

Initial conditions

Thermal system

The mechanism is detailed for the thermal system but the same mechanism can be used for user-defined equations. In our example, the name of the equation is defined in the macro CS_THERMAL_EQNAME

{
cs_equation_param_t *eqp = cs_equation_param_by_name(CS_THERMAL_EQNAME);
/* Define the initial conditions */
/* ----------------------------- */
/* If nothing is done, then a zero value is set by default */
cs_equation_add_ic_by_analytic(eqp,
nullptr, /* all cells */
_initial_temperature, /* function def. */
nullptr); /* no context */
}

where the function _initial_temperature has a predefined prototype (cf. the definition of the function pointer cs_analytic_func_t)

static void
_initial_temperature(cs_real_t time,
cs_lnum_t n_elts,
const cs_lnum_t *elt_ids,
const cs_real_t *coords,
bool dense_output,
void *input,
cs_real_t *retval)
{
CS_NO_WARN_IF_UNUSED(time);
CS_NO_WARN_IF_UNUSED(input);
if (elt_ids == nullptr) { /* No indirection */
for (cs_lnum_t i = 0; i < n_elts; i++)
retval[i] = -1 + 2*coords[3*i]; /* T(t=0) = -1 + 2*x */
}
else {
if (dense_output)
for (cs_lnum_t i = 0; i < n_elts; i++)
retval[i] = -1 + 2*coords[3*elt_ids[i]]; /* T(t=0) = -1 + 2*x */
else {
for (cs_lnum_t i = 0; i < n_elts; i++) {
const cs_lnum_t elt_id = elt_ids[i];
retval[elt_id] = -1 + 2*coords[3*elt_id]; /* T(t=0) = -1 + 2*x */
}
} /* dense_output ? */
} /* elt_ids == nullptr ? */
}

GWF module

Here is another example extracted from the file cs_user_parameters-cdo-gwf.c (in src/user_examples) but this is readily applicable to any equation.

{
/* Define the initial condition with an analytic function (if nothing is
done, the default initialization is zero) */
cs_equation_add_ic_by_analytic(t_eqp, "cells", get_tracer_ic, nullptr);
}

where the function get_tracer_ic has a predefined prototype (cf. the definition of the function pointer cs_analytic_func_t)

static inline void
get_tracer_ic(cs_real_t time,
cs_lnum_t n_elts,
const cs_lnum_t *pt_ids,
const cs_real_t *xyz,
bool dense_output,
void *input,
cs_real_t *retval)
{
CS_UNUSED(input);
/* Physical parameters */
const double magnitude = 2*k1/(k1 + k2);
const double x_front = magnitude * time;
/* Fill retval array */
for (cs_lnum_t i = 0; i < n_elts; i++) {
const cs_lnum_t id = (pt_ids == nullptr) ? i : pt_ids[i];
const cs_lnum_t r_id = (dense_output) ? i : id;
const double x = xyz[3*id];
if (x <= x_front)
retval[r_id] = 1;
else
retval[r_id] = 0;
} /* Loop on selected elements */
}

Definition of properties

User-defined properties

When a property has been added, the second step is to define this property. According to the type of property (isotropic, orthotropic or anisotropic) definitions differ. Here are two examples:

{
cs_property_t *conductivity = cs_property_by_name("conductivity");
cs_real_33_t tensor = {{1.0, 0.5, 0.0}, {0.5, 1.0, 0.5}, {0.0, 0.5, 1.0}};
cs_property_def_aniso_by_value(conductivity, // property structure
"cells", // name of the volume zone
tensor); // values of the property
cs_property_t *rhocp = cs_property_by_name("rho.cp");
cs_real_t iso_val = 2.0;
cs_property_def_iso_by_value(rhocp, // property structure
"cells", // name of the volume zone
iso_val); // value of the property
}

Thermal system

The mechanism is the same as for user-defined properties. The named are predefined and associated to the following macros:

{
/* Define the predefined properties */
/* -------------------------------- */
cs_property_t *lambda = cs_property_by_name(CS_THERMAL_LAMBDA_NAME);
cs_property_def_iso_by_value(lambda, "D1", 1.0);
cs_property_def_iso_by_value(lambda, "D2", 2.5);
cs_property_t *cp = cs_property_by_name(CS_THERMAL_CP_NAME);
cs_property_def_iso_by_value(cp, nullptr, 1); /* null means all cells */
cs_property_t *rho = cs_property_by_name(CS_PROPERTY_MASS_DENSITY);
cs_property_def_iso_by_value(rho, nullptr, 1979);
}

Definition of an advection field

When an advection field has been added, the second step is to define this advection field. Here are is an example of definition using an anlytic function and the activation of optional features:

{
cs_adv_field_t *adv = cs_advection_field_by_name("adv_field");
cs_advection_field_def_by_analytic(adv, _define_adv_field, nullptr);
}

Definition of source terms

User-defined equation

A first simple example.

{
cs_equation_param_t *eqp = cs_equation_param_by_name("AdvDiff.Upw");
/* Simple definition with cs_equation_add_source_term_by_val
where the value of the source term is given by m^3
*/
cs_real_t st_val = -0.1;
cs_equation_add_source_term_by_val(eqp, "cells", &st_val);
}

The second example shows an advanced usage relying on an analytic function and an input structure. Moreover, a more accurate quadrature rule is specified.

{
/* More advanced definition relying on an analytic function and a context
structure */
cs_equation_param_t *eqp2 = cs_equation_param_by_name("MyEq");
double *input = nullptr;
CS_MALLOC(input, 2, double);
input[0] = 0.5; /* Value of the reaction coefficient */
input[1] = 4.0*atan(1.0); /* Value of pi (computed only once) */
cs_xdef_t *st =
cs_equation_add_source_term_by_analytic(eqp2,
"x_leq_0", /* zone name */
_my_source_term,
input); /* context structure */
/* Specify how the cs_xdef_t structure can free its input structure */
cs_xdef_set_free_input_function(st, _free_input);
/* st can be used for advanced settings like quadrature rules. By default,
a barycentric quadrature rule is used (one evaluation at the cell center
by mesh cell) */
cs_xdef_set_quadrature(st, CS_QUADRATURE_HIGHER);
/* Each cell is subdivided into an implicit tetrahedral sub-mesh relying on
the vertices, the middle of each edge, the face barycenter and the cell
center. A quadrature exact up to 3rd order polynomial is set. */
}

The user-defined function to compute the source term is specified as follows

static void
_my_source_term(cs_real_t time,
cs_lnum_t n_pts,
const cs_lnum_t *pt_ids,
const cs_real_t *xyz,
bool dense_output,
void *input,
cs_real_t *values)
{
CS_NO_WARN_IF_UNUSED(time);
const double *pcoefs = (double *)input;
const double mu = pcoefs[0];
const double pi = pcoefs[1];
for (cs_lnum_t i = 0; i < n_pts; i++) {
const cs_lnum_t id = (pt_ids == nullptr) ? i : pt_ids[i];
const cs_lnum_t ii = dense_output ? i : id;
const double x = xyz[3*id], y = xyz[3*id+1], z = xyz[3*id+2];
const double px = pi*x, cpx = cos(px), spx = sin(px);
const double py = 2*pi*y, cpy = cos(py), spy = sin(py);
const double pz = pi*z, cpz = cos(pz), spz = sin(pz);
const cs_real_t gx = cpx*spy*spz;
const cs_real_t gy = 2*spx*cpy*spz;
const cs_real_t gz = spx*spy*cpz;
values[ii] = pi*( (y-0.5)*gx + (0.5-x)*gy + (z+1.0)*gz ) + mu*spx*spy*spz;
}
}

and the function for the memory management of a cs_xdef_t structure is

static void *
_free_input(void *input)
{
double *_input = (double *)input;
CS_FREE(_input);
input = nullptr;
return nullptr;
}

Add diffusion, advection, etc. to a user-defined equation

Add terms to an equation like a diffusion term, an advection term, unsteady term, reaction terms.

{
/* Retrieve the set of equation parameters of the equation to modify */
cs_equation_param_t *eqp = cs_equation_param_by_name("AdvDiff.Upw");
/* Add an unsteady term (draw a link between this equation and a
property) */
cs_property_t *rhocp = cs_property_by_name("rho.cp");
cs_equation_add_time(eqp, rhocp);
/* Add a diffusion term (draw a link between this equation and a
property) */
cs_property_t *conductivity = cs_property_by_name("conductivity");
cs_equation_add_diffusion(eqp, conductivity);
/* Add an advection term (draw a link between this equation and an
advection field) */
cs_adv_field_t *adv = cs_advection_field_by_name("adv_field");
cs_equation_add_advection(eqp, adv);
}

In some cases, one can also add less common terms such as a 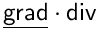$\mathsf{\underline{grad}\cdot div}$ or $\mathsf{\underline{curl}\cdot\underline{curl} }$ (only available with CDO edge_based schemes).

{
/* Retrieve the set of equation parameters of the equation to modify */
cs_equation_param_t *eqp = cs_equation_param_by_name("MyEq");
/* Add a curl-curl term (draw a link between this equation and a
property) */
cs_property_t *mu = cs_property_by_name("mu");
cs_equation_add_curlcurl(eqp,
mu,
false); /* reciprocal of the property */
/* Add a grad-div term (draw a link between this equation and a
property) */
cs_property_t *gamma = cs_property_by_name("gamma");
cs_equation_add_graddiv(eqp, gamma);
}

Settings done in cs_user_parameters()

Logging options

The management of the level and frequency of details written by the solver can be specified for CDO/HHO schemes as follows:

{
/* Manage the output logging/checkpoint
* ====================================
* - log frequency in the run_solver.log
* - level of verbosity (-1: no, 0, 1, higher is for debugging purpose)
* - checkpoint/restart frequency
*/
cs_domain_set_output_param(domain,
CS_RESTART_INTERVAL_ONLY_AT_END,
10, /* log frequency */
2); /* verbosity */
}

Time stepping strategy

The management of the time step with CDO/HHO schemes can be specified as follows:

{
/* Time step management
* ====================
* If there is an inconsistency between the max. number of iteration in
* time and the final physical time, the first condition encountered stops
* the calculation.
*/
cs_domain_set_time_param(domain,
100, /* nt_max or -1 (automatic) */
-1.); /* t_max or < 0. (automatic) */
/* Define the value of the time step. Two functions are available to do
this:
1. cs_domain_def_time_step_by_value(domain, dt_val);
2. cs_domain_def_time_step_by_func(domain, dt_func);
The second way enables more complex definitions of the time step.
*/
cs_domain_def_time_step_by_value(domain, 1.0);
}

This can be completed with numerical options to specify the time scheme. See the next section)

Discretization parameters associated to an equation

To modify the numerical settings, the mechanism relies on a (key, value) rationale. The function to use is cs_equation_param_set For instance, with an equation called "MyEquation", and a key called CS_EQKEY_PARAM_TO_SET with the value "value_to_set".

cs_equation_param_t *eqp = cs_equation_param_by_name("MyEquation");
cs_equation_param_set(eqp, CS_EQKEY_PARAM_TO_SET, "value_to_set");
cs_equation_param_by_name
cs_equation_param_t * cs_equation_param_by_name(const char *eqname)
Return the cs_equation_param_t structure associated to a cs_equation_t structure based on the equatio...
Definition cs_equation.cpp:600
cs_equation_param_set
void cs_equation_param_set(cs_equation_param_t *eqp, cs_equation_key_t key, const char *keyval)
Set a parameter attached to a keyname in a cs_equation_param_t structure.
Definition cs_equation_param.cpp:1483
cs_equation_param_t
Set of parameters to handle an unsteady convection-diffusion-reaction equation with term sources.
Definition cs_equation_param.h:193

If one wants to modify the settings for all equations, this is possible using the function cs_equation_set_default_param

cs_equation_set_default_param(CS_EQKEY_PARAM_TO_SET, "value_to_set");
cs_equation_set_default_param
void cs_equation_set_default_param(cs_equation_key_t key, const char *keyval)
Set a parameter attached to a keyname for the default settigns.
Definition cs_equation.cpp:1855

All available keys are listed and described with cs_equation_key_t One gives some examples for some of them.

Set the space discretization scheme

The key is CS_EQKEY_SPACE_SCHEME with the possible value gathered in the following table

key_value description
"cdo_vb" or "cdovb" Switch to a CDO vertex-based discretization (degrees of freedom are located at the mesh vertices). One value per vertex in the case of scalar-valued equation and three values per vertex in the case of a vector-valued equation.
"cdo_vcb" or "cdovcb" Switch to a CDO vertex+cell-based discretization (degrees of freedom are located at the mesh vertices and at the mesh cells). One value per vertex and per cell in the case of scalar-valued equation and three values per vertex and pêr cell in the case of a vector-valued equation. Thanks to a static condensation operation, the algebraic system is reduced to only vertex unknows.
"cdo_fb" or "cdofb" Switch to a CDO face-based discretization (degrees of freedom are located at interior and boundary faces and at mesh cell). One value per face and mesh cell in the case of scalar-valued equation and three values per face and mesh cell in the case of a vector-valued equation. Thanks to a static condensation operation, the algebraic system is reduced to only face unknows.
"cdo_cb" or "cdocb" Switch to a CDO cell-based discretization (degrees of freedom are located at mesh cells for the potential and at faces for the flux). Only scalar-valued equation are possible. One value per cell for the potential. One value per face for the flux unknown (the normal component of the flux).
"cdo_eb" or "cdoeb" Switch to CDO edge-based discretization (degrees of freedom are located at mesh edges, one scalar per edge corresponding to the circulation). Only vector-valued equation are handled with this discretization.
"hho_p0" Switch to a HHO(k=0) discretization relying on $P_0$ polynomial approximation. (degrees of freedom are located at interior and boundary faces and at mesh cells). One value per face and per mesh cell in the case of scalar-valued equation and three values per face and mesh cell in the case of a vector-valued equation. Thanks to a static condensation operation, the algebraic system is reduced to only face unknows.
"hho_p1" Switch to a HHO(k=1) discretization relying on $P_1$ polynomial approximation. (degrees of freedom are located at interior and boundary faces and at mesh cells). Three values per face and four values per cell in the case of scalar-valued equation and nine values per face and 12 values per cell in the case of a vector-valued equation. Thanks to a static condensation operation, the algebraic system is reduced to only face unknows.
"hho_p2" Switch to a HHO(k=2) discretization relying on $P_2$ polynomial approximation. (degrees of freedom are located at interior and boundary faces and at mesh cells). Six values per face and ten values per cell in the case of scalar-valued equation and 18 values per face and 30 values per cell in the case of a vector-valued equation. Thanks to a static condensation operation, the algebraic system is reduced to only face unknows.

An example of usage:

{
cs_equation_param_t *eqp = cs_equation_param_by_name("MyEq");
cs_equation_param_set(eqp, CS_EQKEY_SPACE_SCHEME, "cdo_fb");
}

More details can be found in [4] for CDO-Vb, CDO-Fb, CDO-Cb and CDO-Eb. CDO-Fb are also detailed in [15]. CDO-VCb are detailed in [7]

Set the advection scheme

{
cs_equation_param_t *eqp = cs_equation_param_by_name("AdvDiff.Upw");
/* Set the advection scheme */
cs_equation_param_set(eqp, CS_EQKEY_ADV_SCHEME, "upwind");
/* Set the advection formulation
- "u.grad(Y)" for a "non-conservative" or gradient formulation
- "div(u.Y)" for a "conservtive" or divergence formulation
*/
cs_equation_param_set(eqp, CS_EQKEY_ADV_FORMULATION, "non_conservative");
}

The available advection schemes are listed in the description of the key CS_EQKEY_ADV_SCHEME

key value description type available with
"upwind" first order upwind scheme (convergence rate is equal to 0.5 on pure advection problem with a solution having a low regularity). This is the most robust choice. This yields a high-level of numerical diffusion. Thus, when the Péclet number (ratio between convection and diffusion) is low, a centered scheme or a scheme with less upwinding is a better choice in terms of accuracy CS_PARAM_ADVECTION_SCHEME_UPWIND CDO vb, CDO fb
"centered" second-order scheme on sufficiently regular solution. Dispersivity issue can occur with this scheme. This is not a good choice when the problem is dominated by the convection term. CS_PARAM_ADVECTION_SCHEME_CENTERED CDO vb, CDO fb
"mix_centered_upwind", "hybrid_centered_upwind" This is a hybrid advection scheme mixing an upwind and a centered advection scheme. The portion of upwinding (between 0. and 1.) is set thanks to the key CS_EQKEY_ADV_UPWIND_PORTION By default, the value 0.15 is used (0.25 when the GWF module is activated). CS_PARAM_ADVECTION_SCHEME_HYBRID_CENTERED_UPWIND CDO vb
"cip" "Continuous Interior Penalty" scheme detailed in [7] This scheme is only available with a non conservative or gradient formulation of the advective term. A switch to this formulation is automatically done. This a second-order scheme on regular solutions with a built-in stabilization relying on the jump of the gradient. The scaling in front of the stabilization term is computed automatically but it can be modified by the user thanks to the key CS_EQKEY_ADV_CIP_COEF CS_PARAM_ADVECTION_SCHEME_CIP CDO vcb
"cip_cw" Same as the "cip" but the advective field is assumed to be constant in each cell. This enables further optimizations when building the advection matrix. CS_PARAM_ADVECTION_SCHEME_CIP_CW CDO vcb
"samarskii" This scheme shares some similarities with a "hybrid_centered_upwind" scheme since a portion of upwinding is added to a centered scheme. This portion smoothly varies between mesh cells according to the evaluation of a local Péclet number. A function (the samarskii one) relates the Péclet number to the level of upwinding. CS_PARAM_ADVECTION_SCHEME_SAMARSKII CDO vb
"sg" SG means "Scharfetter Gummel". This is as a Samarskii scheme. The difference holds in the function computing the portion of upwinding from a local Péclet number. CS_PARAM_ADVECTION_SCHEME_SG CDO vb

Here is a second set of examples

{
cs_equation_param_t *eqp1 = cs_equation_param_by_name("Eq1");
/* Set the advection scheme */
cs_equation_param_set(eqp1, CS_EQKEY_ADV_SCHEME, "mix_centered_upwind");
/* Set the portion of upwinding to add to a centered scheme. The same
portion is added in the whole domain (contrary to the "sg" or
"samarskii" advection scheme) */
cs_equation_param_set(eqp1, CS_EQKEY_ADV_UPWIND_PORTION, "0.45");
/* It's possible to set automatically the upwinding portion using a
Scharfetter-Gummel scheme or the Samarskii scheme. These two advection
schemes differ on the weighting function used to compute the portion of
upwinding. In both cases, one uses an estimation of the local Péclet
number to evaluate the needed portion of upwinding. */
cs_equation_param_t *eqp_sg = cs_equation_param_by_name("Eq2_SG");
cs_equation_param_set(eqp_sg, CS_EQKEY_ADV_SCHEME, "sg");
cs_equation_param_t *eqp_sa = cs_equation_param_by_name("Eq2_SA");
cs_equation_param_set(eqp_sa, CS_EQKEY_ADV_SCHEME, "samarskii");
/* In case of a CDO-VCb schemes, one sets a CIP scheme and then modify the
scaling coefficient in front of the stabilization term */
cs_equation_param_t *eqp_vcb = cs_equation_param_by_name("Eq3_CIP");
cs_equation_param_set(eqp_vcb, CS_EQKEY_ADV_SCHEME, "cip");
cs_equation_param_set(eqp_vcb, CS_EQKEY_ADV_CIP_COEF, "1");
}

There is no advection scheme available with HHO schemes or CDO cb and CDO eb schemes up to now.

Set the time scheme

When the equation to solve is unsteady, one has to specify a time discretization scheme. Available time schemes are listed in the description of the key CS_EQKEY_TIME_SCHEME By default, a first order implicit Euler scheme is used. To modify this default settings, please proceed as follows:

{
cs_equation_param_t *eqp1 = cs_equation_param_by_name("Eq1");
/* Set the time scheme */
cs_equation_param_set(eqp1, CS_EQKEY_TIME_SCHEME, "theta_scheme");
/* When a theta-scheme is used. It is possible to specify the value of the
theta weighting (value should be between 0 and 1 */
cs_equation_param_set(eqp1, CS_EQKEY_TIME_THETA, "0.57");
}

The mass matrix associated to the unsteady term is also a parameter. One can use either a mass matrix like in FV scheme using a "voronoi" algorithm (default) or the "wbs" algorithm like in Finite Element (FE) schemes.

{
cs_equation_param_t *eqp_fe = cs_equation_param_by_name("Eq_FE_like");
/* Set the algorithm to build the Hodge operator related to the unsteady
term. This is the same as defining the mass matrix in Finite Element
schemes */
cs_equation_param_set(eqp_fe, CS_EQKEY_HODGE_TIME_ALGO, "wbs");
/* The other choice */
cs_equation_param_t *eqp_fv = cs_equation_param_by_name("Eq_FV_like");
cs_equation_param_set(eqp_fv, CS_EQKEY_HODGE_TIME_ALGO, "voronoi");
}

Modify the numerical scheme for the diffusion term

Several algorithms are available to build the diffusion term. They are all listed in the description of the key CS_EQKEY_HODGE_DIFF_ALGO Please refer to [4] for more details In the case of the cost (or ocs), one can specify the value of the scaling coefficient in front of the stabilization part. This is done using the key CS_EQKEY_HODGE_DIFF_COEF

{
cs_equation_param_t *eqp = cs_equation_param_by_name("MyEq");
/* Modify other parameters than the space discretization */
cs_equation_param_set(eqp, CS_EQKEY_HODGE_DIFF_ALGO, "cost");
cs_equation_param_set(eqp, CS_EQKEY_HODGE_DIFF_COEF, "dga");
}

Linear algebra settings

Many options are available in code_saturne to specify the way to solve a linear system. This is detailed here for the CDO/HHO part.

To go further

The detailed description of CDO schemes, the mathmatical analysis and numerical results on benchmarks are available in the following PhD thesis:

Additional publications :