Introduction

Two classical models are available in code_saturne for rotor/stator interactions modelling in turbomachinery computations: the steady approach which is based on the so-called Frozen Rotor modelling and the transient rotor/stator approach which is based on a sliding mesh technique.

Warning: This page describes these functionalities based on a single code_saturne computation. An alternative rotor/stator coupling based on the code/code coupling of code_saturne with itself is still possible (and briefly described in this page) but it is not recommended (will be highly modified soon).

Mesh requirements

Periodicity

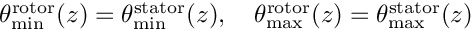The rotational periodicity treatment is possible only in Frozen Rotor. However, the interface plane between rotor and stator must match in the azimutal $\theta$ direction: $\theta_{\text{min}}^{\text{rotor}}(z)=\theta_{\text{min}}^{\text{stator}}(z),\quad\theta_{\text{max}}^{\text{rotor}}(z)=\theta_{\text{max}}^{\text{stator}}(z)$ for all z through the rotation axis direction.

Rotor/stator interface

Transient rotor/stator: in the input mesh(es), the interface between rotor and stator domains has to be composed of boundary faces. Then the inteface boundary faces are joined during the computation and transformed into internal faces, as the preprocessing step can do in usual calculations. The classical way to fulfill this requirement is to provide separate meshes for each rotor or stator domains, but placing both sections in the same mesh is allowed, as long as they are topologically disjoint.
Frozen Rotor: the interface can be composed of boundary faces (then the inteface boundary faces are joint at the beginning of the computation and turn into internal faces) or internal faces.

Data setting

The data setting is made through the GUI or through the cs_user_turbomachinery.c source file. Through the latter, the type of turbomachinery model can be first set in cs_user_turbomachinery function:

 
  /* Set turbomachinery model type:
 
     CS_TURBOMACHINERY_NONE,          No turbomachinery modeling
     CS_TURBOMACHINERY_FROZEN,        Frozen rotor model
     CS_TURBOMACHINERY_TRANSIENT      Full transient simulation
  */
 
  cs_turbomachinery_set_model(CS_TURBOMACHINERY_TRANSIENT);
 

Then, the rotor region and the rotor/stator interface boundaries has to be specified in cs_user_turbomachinery_rotor function. The rotor region is first specified, as follows:

  {
    /* Define cells belonging to rotor and associated axis */
 
    double rotation_velocity = 2.;
    double rotation_axis[3] = {0., 0., 1.};
 
    double rotation_invariant[3] = {0., 0., 0.};
 
    const char cell_criteria[]  = "cylinder[0.0, 0.0, 0.0,"
                                          " 0.0, 0.0, 1.0,"
                                          " 2.0]";
 
    cs_turbomachinery_add_rotor(cell_criteria,
                                rotation_velocity,
                                rotation_axis,
                                rotation_invariant);
 
  }

In this example, rotation_velocity refers to the rotation angular velocity of the rotor, in rad/s. The rotation axis can be normalized (it is eventually normalized afterwards by the code). Note that if a rotor is added, the code appends an instance of cs_rotation_t structure in the global list of rotors (see Basic operations section in the following).

Then the rotor/stator interface boundary is specified. This step is mandatory only for the CS_TURBOMACHINERY_TRANSIENT model. For the CS_TURBOMACHINERY_FROZEN model, this step is required only if the interface is made of boundary faces (see Rotor/stator interface subsection above).

  {
    /* Define joining associated with rotor/stator interface */
 
    const char faces_criteria[] = "rotor_interface or stator_interface";
 
    int    verbosity = 0;     /* per-task dump if > 1, debug level if >= 3 */
    int    visualization = 0; /* debug level if >= 3 */
    float  fraction = 0.10, plane = 25.;
 
    cs_turbomachinery_join_add(faces_criteria,
                               fraction,
                               plane,
                               verbosity,
                               visualization);
 
    /* Note that advanced parameters may be defined using the function
       cs_join_set_advanced_param(), just as for regular joinings or
       periodicities. In this case, retrieve the joining number from the
       previous call. */
 
  }

The rotation velocity can be modified during the calculation. The following example shows how to set a linearly increasing rotation velocity in cs_user_turbomachinery_set_rotation_velocity function:

  {
    /* Linearly increase the rotation velocity from 0 to 1470 rd/min in 0.2 s */
    /* ---------------------------------------------------------------------- */
 
    int rotor_num = 1;
    double two_pi = 2. * acos(-1.);
    double rotation_velocity = -1470. * two_pi / 60.;
    double rotor_vel =   rotation_velocity
                       * cs_math_fmin(cs_glob_time_step->t_cur / 0.2, 1.);
 
    cs_turbomachinery_set_rotation_velocity(rotor_num,
                                            rotor_vel);
  }

User recomandations

Meshing recomandations at interface

As mentioned above, when a rotor/stator inteface boundary exists (in particular for the CS_TURBOMACHINERY_TRANSIENT model), it is then joined by the solver during the computation. It is thus important to be aware that the success of a joining operation is strongly dependant on the quality of the mesh at the interface. More precisely, the refinement must be as similar as possible on both sides of the interface. Moreover, it is reminded that the tolerance parameter of a joining is a fraction of the shortest edge linked with a vertex to join. Consequently, cells where the refinement in the azimutal $\theta$ direction is much coarser than those in one of the two others can also lead to a joining failure. In particular, the user should be wary of boundary layers.

Remarks

The tolerance parameter of a joining should always be lower than 0.5.
If the meshes at both sides of the interface are very different such that the joining fails, advanced joining parameters are available. However, modifying the mesh is more likely to succeed. The introduction of some kind of buffer cells layer on both sides of the interface is strongly recommended. Ideally, each of the two layers should have the same refinement and a constant azimutal step (this latter recommandation is relevant only for CS_TURBOMACHINERY_TRANSIENT model).

Alternative rotor/stator coupling

If the meshes on both sides of the interface are very different and can not be modified, the user should turn to a rotor/stator coupling based on the code/code coupling of code_saturne with itself. This simply requires replacing the definition of a face joining for an interface (using the GUI or a call to cs_turbomachinery_join_add by a call to cs_turbomachinery_coupling_add.

If a coupling is defined and the rotation is not null in at least one of the cases, icorio determines the type of rotor/stator coupling: icorio = 1 for a Frozen Rotor computation and icorio = 0 for a sliding mesh approach.

Warning: Contrary to the mesh joining approach, the code/code coupling approach is not fully conservative.

User operations

Basic operations

A specific rotor is identified by an integer value. The "default rotor" is actually the stator that is the fixed part of the domain, with identifier 0. Then the identifiers of the rotors are incremented as the user add rotors (cs_turbomachinery_add_rotor, see above).

Local definitions and initialization

 
  /* Mesh-related variables */
 
  const cs_lnum_t n_b_faces = domain->mesh->n_b_faces;
 
  const cs_real_3_t  *restrict cell_cen
    = (const cs_real_3_t *)domain->mesh_quantities->cell_cen;
 
  /* 0. Initialization
     ================= */
 
  /* Local constants defintion */
 
  const cs_real_t _PI = acos(-1.);
  const cs_real_t _G = 9.81;
 
  /* Flow properties */
 
  double ro0 = cs_glob_fluid_properties->ro0;
  cs_real_t flowrate = 0.238;

Once the rotor identifier is known, access to its parameters as follows:

 
  /* Access to a specific rotation zone (the first one) */
 
  cs_lnum_t rotor_id = 1;
  const cs_rotation_t *ref_rot = cs_glob_rotation + rotor_id;
 
  /* Rotation zone parameters */
 
  double omega = ref_rot->omega;         /* angular velocity [rad/s] */
  cs_real_3_t axis = {ref_rot->axis[0],  /* rotation axis (normalized vector) */
                      ref_rot->axis[1], ref_rot->axis[2]};

Importantly, the rotor associated to each cell of the domain can be retrieved thanks to a rotor identifier list as follows:

 
  const int *rotor_num = nullptr;
  rotor_num = cs_turbomachinery_get_cell_rotor_num();
 
  for (cs_lnum_t cell_id = 0; cell_id < n_cells; cell_id++) {
    cs_rotation_t *rot = cs_glob_rotation + rotor_num[cell_id];
    /* ... */
 

Turbomachinery dedicated postprocessing functions

Useful postprocessing functions relative to the machinery characteristics are available: postprocessing of the couple on the rotor walls (cs_post_moment_of_force) and postprocessing of the head generated by the machinery (cs_post_turbomachinery_head). In the latter one, the mesh locations (CS_MESH_LOCATION_CELLS, CS_MESH_LOCATION_BOUNDARY_FACES or CS_MESH_LOCATION_INTERNAL_FACES) associated with the given selection criteria must be specified.

 
  /* Postprocessing of the couple: axial moment resulting from the stresses */
  /* on the rotor blades */
 
  cs_lnum_t n_elts;
  cs_lnum_t *elt_list;
 
  BFT_MALLOC(elt_list, n_b_faces, cs_lnum_t);
  cs_selector_get_b_face_list("rotor_blades", &n_elts, elt_list);
 
  cs_real_t c = cs_post_moment_of_force(n_elts, elt_list, axis);
 
  BFT_FREE(elt_list);
 
  /* Postprocessing of the head: total pressure increase through the machinery */
 
  cs_real_t turbomachinery_head
    = cs_post_turbomachinery_head
        ("inlet",                          /* selection criteria at suction */
         CS_MESH_LOCATION_BOUNDARY_FACES,  /* associated mesh location */
         "z > 2.725 and z < 2.775",        /* selection criteria at discharge */
         CS_MESH_LOCATION_CELLS);          /* associated mesh location */
 

Velocity profiles extraction in cylindrical coordinates

Below is another example showing how to extract velocity profile in cylindrical coordinates.

 
  if (domain->time_step->nt_cur == domain->time_step->nt_max){
 
    cs_real_3_t *vel = (cs_real_3_t *)CS_F_(vel)->val;
 
    cs_field_t *f_mom_wr = nullptr, *f_mom_wt = nullptr;
 
    /* In case of transient rotor/stator computation, the moments for
       the velocity in cylindrical coordinates are assumed to be defined
       in the dedicated user file (cs_user_parameters.c, see the user example
       for time moments definition) */
 
    cs_turbomachinery_model_t tbm_model = cs_turbomachinery_get_model();
 
    if (tbm_model == CS_TURBOMACHINERY_TRANSIENT) {
      f_mom_wr = cs_time_moment_get_field(1);
      f_mom_wt = cs_time_moment_get_field(2);
    }
 
    FILE *f1 = nullptr, *f2 = nullptr;
 
    /* Only process of rank 0 (parallel) or -1 (scalar) writes to this file. */
 
    if (cs_glob_rank_id <= 0) {
 
      f1 = fopen("Wr_mean.dat","w");
      fprintf(f1, "# %17s%17s\n", "angle", "Wr");
 
      f2 = fopen("Wt_mean.dat","w");
      fprintf(f2, "# %17s%17s\n", "angle", "Wt");
    }
 
    cs_real_t radius = 0.214;
    cs_real_t axicoo = 2.e-2;
 
    cs_lnum_t npoint = 360;
    cs_lnum_t cell_id1 = -999;
    int       rank_id1 = -999;
 
    for (cs_lnum_t point_id = 0; point_id < npoint; point_id++) {
 
      cs_real_t xth0 = -_PI/npoint;
      cs_real_3_t xyz = {radius*cos(xth0 - (double)point_id/npoint*2.*_PI),
                         radius*sin(xth0 - (double)point_id/npoint*2.*_PI),
                         axicoo};
 
      cs_lnum_t cell_id, rank_id;
 
      /* Find the closest cell in this rotor */
      _findpt_r(domain, ref_rot, xyz, &cell_id, &rank_id);
 
      if ((cell_id != cell_id1) || (rank_id != rank_id1)) {
        cell_id1 = cell_id;
        rank_id1 = rank_id;
 
        cs_real_t xr, xtheta, xvr, xvt;
 
        /* Set temporary variables for the process containing
         * the point and then send it to other processes. */
        if (cs_glob_rank_id == rank_id) {
 
          /* Radius (first component of the x vector in cylindrical coords) */
          cs_real_t xc[3];
          cs_rotation_cyl_v(ref_rot, cell_cen[cell_id], cell_cen[cell_id], xc);
          xr = xc[0];
 
          /* Angle in [0, 2pi] */
          double xthet1, xthet2;
          xthet1 = acos((cell_cen[cell_id][0] - ref_rot->invariant[0])/xr);
          xthet2 = asin((cell_cen[cell_id][1] - ref_rot->invariant[1])/xr);
          if (xthet2 > 0)
            xtheta = xthet1;
          else if (xthet1 < _PI/2.)
            xtheta = 2.*_PI + xthet2;
          else
            xtheta = _PI - xthet2;
 
          if (tbm_model == CS_TURBOMACHINERY_FROZEN) {
            cs_real_3_t xvc;
            cs_rotation_cyl_v(ref_rot, cell_cen[cell_id], vel[cell_id], xvc);
            xvr = xvc[0];
            /* Relative tangential velocity */
            xvt = xvc[1] - omega*xr;
          }
          else {
            xvr = f_mom_wr->val[cell_id];
            xvt = f_mom_wt->val[cell_id];
          }
 
        } else {
          xtheta = 0.;
          xvr = 0.;
          xvt = 0.;
        }
 
        /* Broadcast to other ranks in parallel */
        cs_real_t bp[] = {xtheta, xvr, xvt};
        cs_parall_bcast(rank_id, 3, CS_REAL_TYPE, bp);
        xtheta = bp[0], xvr = bp[1], xvt = bp[2];
 
        if (cs_glob_rank_id <= 0) {
          fprintf(f1,"  %17.9e%17.9e\n", xtheta, xvr);
          fprintf(f2,"  %17.9e%17.9e\n", xtheta, xvt);
        }
      }
 
    } /* end of loop on point_id */
    if (cs_glob_rank_id <= 0) {
      fclose(f1);
      fclose(f2);
    }
 
  } /* end of if statement on current time step */
 

Fortran naming

Useful fortran variables and/or functions specific to turbomachinery computations are contained int the fortran module turbomachinery and rotation.