7.1
general documentation
Solving a heat equation with a user solver (cs_user_solver.c)

Introduction

C user functions for the setting of a user solver. The cs_user_solver function allows one to replace the Code_Saturne solver by a solver of his own.

The following example shows the setting of a user solver which solves a heat equation with the finite volume method.

Activating the user solver

If the function cs_user_solver_set returns 1, the Code_Saturne solver is replaced by the solver defined in cs_user_solver .

int
cs_user_solver_set(void)
{
return 1;
}

User solver implementation

Variable declaration

The following variables are declared locally and will be used later in the code. Three pointers to cs_real_t are declared and will stand for the temperature at the time steps n and n-1, and for the analytical solution of the heat equation;

int i, iter, n_iter;
cs_real_t x0, xL, t0, tL;
cs_real_t r;
cs_real_t *t = NULL, *t_old = NULL, *t_sol = NULL;
cs_restart_t *restart, *checkpoint;
cs_time_plot_t *time_plot;
const cs_lnum_t n = mesh->n_cells;
const cs_real_t pi = 4.*atan(1.);
const char var_name[] = "temperature";

Initialization

Three arrays of size n are created. Several constants are initialized, and the array t_old is initialized as follows :

\[ t_{old}(x = i*dx) = sin\frac{pi(0.5+i)}{n}; \]

/* Initialization */
BFT_MALLOC(t, n, cs_real_t);
BFT_MALLOC(t_old, n, cs_real_t);
BFT_MALLOC(t_sol, n, cs_real_t);
x0 = 1.e30;
xL = -1.e30;
for (i = 0; i < mesh->n_b_faces; i++) {
cs_real_t x_face = mesh_quantities->b_face_cog[3*i];
if (x_face < x0) x0 = x_face;
if (x_face > xL) xL = x_face;
}
t0 = 0.;
tL = 0.;
r = 0.2; /* Fourier number */
n_iter = 100000;
for (i = 0; i < n; i++)
t_old[i] = sin(pi*(0.5+i)/n);

Restart creation

One can define a restart computation, as for the real Code_Saturne solver.

/* ------- */
/* Restart */
/* ------- */
restart = cs_restart_create("main.csc", /* file name */
NULL, /* force directory */
CS_RESTART_MODE_READ); /* read mode */
cs_restart_read_section(restart, /* restart file */
var_name, /* buffer name */
1, /* location id */
1, /* number of values per location */
2, /* value type */
t_old); /* buffer */
cs_restart_destroy(&restart);

Time monitoring

Monitoring points can equally be created in order to plot the evolution of the temperature over the time.

/* --------------- */
/* Time monitoring */
/* --------------- */
time_plot = cs_time_plot_init_probe(var_name, /* variable name */
"probes_", /* file prefix */
CS_TIME_PLOT_DAT, /* file format */
true, /* use iter. numbers */
-1., /* force flush */
0, /* buffer size */
1, /* number of probes */
NULL, /* probes list */
NULL, /* probes coord. */
NULL); /* probes names */

Heat equation solving

At each iteration, the new temperature is computed using the Finite Volume Method.

\[ t(x = i \cdot dx) = t_{old}(x = i \cdot dx) + r\cdot(t_{old}(x = (i+1) \cdot dx) - 2 \cdot t_{old}(x = i \cdot dx) + t_{old}(x = (i-1) \cdot dx)) \]

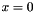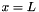The boundary conditions at $ x = 0 $ and $ x = L $ are :

\[ t(x = 0) = t_{old}(x = 0) + r \cdot (t_{old}(x = dx) - 3 \cdot t_{old}(x = 0) + 2 \cdot t_0) \]

\[ t(x = (n-1) \cdot dx) = t_{old}(x = (n-1) \cdot dx) + r \cdot (2 \cdot t_L - 3 \cdot t_{old}(x = (n-1) \cdot dx) + t_{old}(x = (n-2) \cdot dx)) \]

t_old is then updated and t_sol computed. Finally, the temperature at 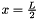$ x = \frac{L}{2} $ and at the current iteration is plotted.

/* ----------- */
/* Calculation */
/* ----------- */
/* Heat equation resolution by Finite Volume method */
for (iter = 0; iter < n_iter; iter++) {
/* 1D Finite Volume scheme, with constant dx */
t[0] = t_old[0] + r*(t_old[1] - 3.*t_old[0] + 2.*t0);
for (i = 1; i < n-1; i++)
t[i] = t_old[i] + r*(t_old[i+1] - 2.*t_old[i] + t_old[i-1]);
t[n-1] = t_old[n-1] + r*(2.*tL - 3.*t_old[n-1] + t_old[n-2]);
/* Update previous value of the temperature */
for (i = 0; i < n; i++)
t_old[i] = t[i];
/* Analytical solution at the current time */
for (i = 0; i < n; i++)
t_sol[i] = sin(pi*(0.5+i)/n)*exp(-r*pi*pi*(iter+1)/(n*n));
/* Plot maximum temperature value (center-value) */
cs_time_plot_vals_write(time_plot, /* time plot structure */
iter, /* current iteration number */
-1., /* current time */
1, /* number of values */
&(t[n/2])); /* values */
}

Checkpoint creation

A checkpoint can be created in order to restart the computation later on.

/* --------- */
/* Chekpoint */
/* --------- */
checkpoint = cs_restart_create("main.csc", /* file name */
NULL, /* force directory */
CS_RESTART_MODE_WRITE); /* write mode */
cs_restart_write_section(checkpoint, /* restart file */
var_name, /* buffer name */
1, /* location id */
1, /* number of values per location */
2, /* value type */
t); /* buffer */
cs_restart_destroy(&checkpoint);

Post-processing

Finally, t and t_sol are postprocessed in order to be compared.

/* --------------- */
/* Post-processing */
/* --------------- */
cs_post_activate_writer(-1, /* default writer */
true); /* activate if 1 */
cs_post_write_var(CS_POST_MESH_VOLUME,
CS_POST_WRITER_ALL_ASSOCIATED,
var_name, /* variable name */
1, /* variable dimension */
false, /* interleave if true */
true, /* define on parents */
CS_POST_TYPE_cs_real_t, /* type */
t, /* value on cells */
NULL, /* value on interior faces */
NULL, /* value on boundary faces */
NULL); /* time-independent output */
cs_post_write_var(CS_POST_MESH_VOLUME,
CS_POST_WRITER_ALL_ASSOCIATED,
"solution", /* variable name */
1, /* variable dimension */
false, /* interleave if true */
true, /* define on parents */
CS_POST_TYPE_cs_real_t, /* type */
t_sol, /* value on cells */
NULL, /* value on interior faces */
NULL, /* value on boundary faces */
NULL); /* time-independent output */

Finalization

/* Finalization */
BFT_FREE(t);
BFT_FREE(t_old);
BFT_FREE(t_sol);
cs_time_plot_finalize(&time_plot);