cs_velocity_pressure_param_t Struct Reference

Inner velocity/pressure iteration options descriptor. More...

#include <cs_velocity_pressure.h>

Collaboration diagram for cs_velocity_pressure_param_t:

Data Fields
int	iphydr
int	icalhy
int	iprco
int	ipredfl
int	irevmc
int	iifren
int	irecmf
int	igprij
int	igpust
int	igrdpp
int	ipucou
int	itpcol
double	arak
int	rcfact
int	staggered
int	nterup
double	epsup
double	xnrmu
double	xnrmu0
double	epsdp
cs_time_control_t	time_control

Detailed Description

Inner velocity/pressure iteration options descriptor.

Members of this structure are publicly accessible, to allow for concise syntax, as they are expected to be used in many places.

Field Documentation

arak

double arak

Arakawa multiplicator for the Rhie and Chow filter (1 by default).

Please refer to the Rhie and Chow filter section of the theory guide for more informations.

epsdp

double epsdp

parameter of diagonal pressure strengthening

epsup

double epsup

relative precision for the convergence test of the iterative process on pressure-velocity coupling

icalhy

int icalhy

compute the hydrostatic pressure in order to compute the Dirichlet conditions on the pressure at outlets

• 1: calculation of the hydrostatic pressure at the outlet boundary
• 0: no calculation of the hydrostatic pressure at the outlet boundary (default) This option is automatically specified depending on the choice of iphydr and the value of gravity (icalhy = 1 if iphydr = 1 and gravity is different from 0; otherwise icalhy = 0). The activation of this option generates an additional calculation cost (about 30% depending on the case).
  If head losses are present just along an outlet boundary, it is necessary to specify icalhy = 0 in order to deactivate the recalculation of the hydrostatic pressure at the boundary, which may otherwise cause instabilities

igprij

int igprij

improve static pressure algorithm

• 1: take -div(rho R) in the static pressure treatment IF iphydr=1
• 0: no treatment (default)

igpust

int igpust

Improved pressure interpolation scheme:

• 1: take user momentum source terms in the static pressure treatment IF iphydr=1
• 0: no treatment (default)

igrdpp

int igrdpp

For the compressible algorithm, indicate whether the pressure should be updated after the solution of the acoustic equation.

• 1: true (default)
• 0: false

iifren

int iifren

indicates the presence of a Bernoulli boundary face (automatically computed)

• 0: no face
• 1: at least one face

iphydr

int iphydr

Improved pressure interpolation scheme. Take into account the balance or imbalance between the pressure gradient and source terms (as gravity and head losses)

• 1: impose the equilibrium of the static part of the pressure with any external force, even head losses (default)
• 2: hydrostatic pressure computation with an apriori momentum equation to obtain a hydrostatic pressure taking into account the imbalance between the pressure gradient and the gravity source term.
• 0: no treatment
  
  When the density effects are important, the choice of iphydr = 1 allows to improve the interpolation of the pressure and correct the non-physical velocities which may appear in highly stratified areas or near horizontal walls.
  The improved algorithm also allows eradicating the velocity oscillations which tend to appear at the frontiers of areas with high head losses.
  In the case of a stratified flow, the calculation cost is higher when the improved algorithm is used (about 30% depending on the case) because the hydrostatic pressure must be recalculated at the outlet boundary conditions: see icalhy.
  On meshes of insufficient quality, in order to improve the convergence, it may be useful to increase the number of iterations for the reconstruction of the pressure right-hand side, i.e. nswrsm.
  If head losses are present just along an outlet boundary, it is necessary to specify icalhy = 0 in order to deactivate the recalculation of the hydrostatic pressure at the boundary, which may otherwise cause instabilities. Please refer to the handling of the hydrostatic pressure section of the theory guide for more information.
  The iphydr = 2 option is a legacy treatment to improve the computation of the pressure gradient for buoyant/stratified flows. In most cases, iphydr = 2 is equivalent to iphydr = 1, but for the following situations, iphydr = 2 can yield better results:
• multiple inlet/outlets with different altitudes
• outlets normal to the gravity Note that iphydr = 2 is less general than iphydr = 1: only gravity forces are taken into account.
  

iprco

int iprco

compute the pressure step thanks to the continuity equation

• 1: true (default)
• 0: false

ipredfl

int ipredfl

Switch on mass flux prediction before momentum solving to be fully conservative in momentum over time for variable density flows.

Deprecated

Will be removed in a future version.

ipucou

int ipucou

indicates the algorithm for velocity/pressure coupling:

• 0: standard algorithm,
• 1: reinforced coupling in case calculation with long time steps
  Always useful (it is seldom advised, but it can prove very useful, for instance, in case of flows with weak convection effects and highly variable viscosity).

irecmf

int irecmf

use interpolated face diffusion coefficient instead of cell diffusion coefficient for the mass flux reconstruction for the non-orthogonalities

• 1: true
• 0: false (default)

irevmc

int irevmc

reconstruction of the velocity field with the updated pressure option

• 0: standard gradient of pressure increment (default)

itpcol

int itpcol

Time scheme option:

• 0: staggered time scheme. On the time grids, the velocity is half a time step behind the density and the buoyant scalar. (See the thesis of [Pierce:2004])
• 1: collocated time scheme. On the time grids, the velocity is at the same location as the density and the buoyant scalar. (See [Ma:2019])

nterup

int nterup

number of iterations on the pressure-velocity coupling on Navier-Stokes

rcfact

int rcfact

Factor of the Rhie and Chow filter:

• 0: dt (by default),
  
• 1: 1/A_u.
  

staggered

int staggered

1D zone simulator option:

• 0: colocated.
  
• 1: staggered.
  

time_control

cs_time_control_t time_control

xnrmu

double xnrmu

norm of the increment 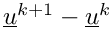of the iterative process on pressure-velocity coupling

xnrmu0

double xnrmu0

norm of

---

The documentation for this struct was generated from the following files:

• src/base/cs_velocity_pressure.h
• src/base/cs_velocity_pressure.cpp