The solidification module relies on CDO face-based schemes.

To set-up a computation taking into account the solidification process, one has to update the cs_user_parameters.c file and edit the function cs_user_model and cs_user_finalize_setup at least in simple cases. In more complex cases, editing the function cs_user_parameters and defining functions to describe the boundary condition or the material properties should be necessary.

Activate the solidification module

The first step is to activate the CDO module in the function cs_user_model (please refer to Activation of CDO/HHO schemes).

When CDO is activated, one can activate the solidification module using cs_solidification_activate. There are eight parameters to set :

The type of solidification model to consider. This implies which equations are to be solved and which variables are involved. Choices are detailed in cs_solidification_model_t ;
An optional flag to specify advanced user-defined options (set 0 if nothing has to be added);
An optional flag to specify automatic post-processing dedicated to this module (set 0 if nothing has to be added);
The domain boundaries (see cs_boundary_t for more details);
The Navier-Stokes model (see cs_navsto_param_model_t for more details). The default choice should be CS_NAVSTO_MODEL_INCOMPRESSIBLE_NAVIER_STOKES but a Stokes model (set CS_NAVSTO_MODEL_STOKES) is also possible if the advection term can be neglected.
Additional user-defined options for the Navier-Stokes model (by default the Boussinesq approximation is set even if 0 is given as parameter). The recommended value for this parameter is 0.
The algorithm used to couple velocity and pressure fields. Available choices are detailed in cs_navsto_param_coupling_t
An optional flag to specify automatic post-processing for the Navier-Stokes module. Available options are detailed in cs_navsto_param_post_bit_t).

  {
    /* For the solidification module:
       cs_solidification_activate(solidification_model_type,
                                  solid_option_flag,
                                  solid_post_flag,
                                  boundaries,
                                  navsto_model,
                                  navsto_model_flag,
                                  navsto_coupling_type,
                                  navsto_post_flag);
 
       If a flag is set to 0, then there is no option to add.
       To add options to a flag:
       flag = option1 | option2 | option3 | ...
    */
 
    cs_flag_t  solid_option_flag = 0;
 
    cs_flag_t  solid_post_flag = CS_SOLIDIFICATION_POST_SOLIDIFICATION_RATE;
 
    cs_flag_t  navsto_model_flag = 0;
 
    cs_flag_t  navsto_post_flag = 0     |
      CS_NAVSTO_POST_VELOCITY_DIVERGENCE |
      CS_NAVSTO_POST_MASS_DENSITY;
 
    /* Activate the solidification module with a binary alloy model (the
       Navier-Stokes and the thermal modules are also activated in back-end) */
 
    cs_solidification_activate(/* Main solidification model */
                               CS_SOLIDIFICATION_MODEL_BINARY_ALLOY,
                               /* Solidification options */
                               solid_option_flag,
                               /* Solidification automatic post options */
                               solid_post_flag,
                               /* NavSto parameters */
                               domain->boundaries,
                               CS_NAVSTO_MODEL_INCOMPRESSIBLE_NAVIER_STOKES,
                               navsto_model_flag,
                               CS_NAVSTO_COUPLING_MONOLITHIC,
                               navsto_post_flag);
 
  }

Model of solidification and its options

Here are listed the available solidification models (first parameter of the function cs_solidification_activate):

CS_SOLIDIFICATION_MODEL_STEFAN : a pure thermal model, i.e. without a fluid motion. A rough phase transition is considered (the solidus is equal to the liquidus temperature) ;
CS_SOLIDIFICATION_MODEL_VOLLER_PRAKASH_87 : a model involving momentum, mass and energy conservation equations. A Boussinesq approximation is used for the Navier–Stokes model. The thermal source term is linearized. A pure component is considered. The solidification process hinges on a head loss described as a Darcy-like source term in the momentum equation (see the Voller and Prakash article for more details).
CS_SOLIDIFICATION_MODEL_VOLLER_NL : This is the CS_SOLIDIFICATION_MODEL_VOLLER_PRAKASH_87 model with a non-linear thermal source term (a Picard algorithm is used to update the source term).
CS_SOLIDIFICATION_MODEL_BINARY_ALLOY : This model hinges on the Voller and Prakash model but adds an additional equation for the solute transport. The solute concentration has an effect on the Boussinesq term. The phase diagram is more complex since a binary alloy is considered. One also handles the eutectic transformation according to the solidification path.

Here are listed the available options (second parameter of the function cs_solidification_activate):

CS_SOLIDIFICATION_NO_VELOCITY_FIELD : This flag disables the resolution of the Navier-Stokes equations. If used with the CS_SOLIDIFICATION_MODEL_VOLLER_PRAKASH_87 and CS_SOLIDIFICATION_MODEL_VOLLER_NL models, this corresponds to a Stefan-like model with a phase transition having a different value for the solidus and liquidus temperatures.
CS_SOLIDIFICATION_WITH_SOLUTE_SOURCE_TERM (only make sense when the model CS_SOLIDIFICATION_MODEL_BINARY_ALLOY is activated). The bulk concentration is treated with a source term related to an explicit advection of the quantity .

Automatic post-processing

Here are listed the available options (third parameter of the function cs_solidification_activate):

The following options make sense only when the CS_SOLIDIFICATION_MODEL_BINARY_ALLOY is activated

Model settings

Set a strategy

Excepted for the Stefan model, it is possible to change the strategy to update quantities such as the way to compute the new thermal source term. There are three strategies available (cs_solidification_strategy_t for more details). The default strategy is CS_SOLIDIFICATION_STRATEGY_LEGACY

CS_SOLIDIFICATION_STRATEGY_LEGACY : Original strategy considered in the Finite Volume scheme
CS_SOLIDIFICATION_STRATEGY_TAYLOR : Update of the thermal source term or the liquid fraction is performed using a Taylor expansion. Only available with a CS_SOLIDIFICATION_MODEL_BINARY_ALLOY
CS_SOLIDIFICATION_STRATEGY_PATH : Update of the thermal source (and of the liquid fraction in case of a CS_SOLIDIFICATION_MODEL_BINARY_ALLOY) relying on the knowledge of the current and previous state.

Here is an example to set the strategy:

  {
    cs_solidification_set_strategy(CS_SOLIDIFICATION_STRATEGY_PATH);
  }

Stefan model

The Stefan model handles the solidification process with the approximation that the liquidus and solidus temperature are the same. Thus, the transition from the solid to liquid or from the liquid to solid is rough.

Voller and Prakash model

The main function to set a Voller and Prakash model is cs_solidification_set_voller_model (follow the link to get a description of the parameters). This function is mandatory and has to be located in cs_user_model after calling cs_solidification_activate

Parameters 1 and 2 correspond to the settings of the Boussinesq term (two coefficients related to a reference temperature and a thermal dilation coefficient in $K^-1\$ ).
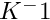Parameters 3 and 4 are the solidus and liquidus temperature describing the behavior of the liquid fraction with respect to the temperature.
Parameters 5 and 6 correspond to the latent heat of the alloy (assumed to be constant) and the secondary dendrite arm spacing (a model parameter taking into account micro-segregation phenomena).

  {
    /* Physical data for the settings a binay alloy model */
 
    cs_real_t  T0 = 0.5, beta_t = 0.01;
    cs_real_t  t_solidus = -0.1, t_liquidus = 0.1;
    cs_real_t  latent_heat = 5, s_das = 0.33541;
 
    /* Set the parameters for the Voller & Prakash model */
 
    cs_solidification_set_voller_model(/* Boussinesq approximation */
                                       beta_t,
                                       T0,
                                       /* Phase diagram */
                                       t_solidus,
                                       t_liquidus,
                                       /* Physical constants */
                                       latent_heat,
                                       s_das);
 
 
    /* If the flag options CS_SOLIDIFICATION_NO_VELOCITY_FIELD has been set,
       then one can use a simplified version of the function */
 
    cs_solidification_set_voller_model_no_velocity(/* Phase diagram */
                                                   t_solidus,
                                                   t_liquidus,
                                                   /* Physical constants */
                                                   latent_heat);
  }

Please notice that a simplified version of the function exists in case of purely thermal model (activated when the flag CS_SOLIDIFICATION_NO_VELOCITY_FIELD has been set).

Non-linear Voller and Prakash model

The setting of the non-linear variant of the Voller and Prakash model relies on the main function as the linear one (i.e. cs_solidification_set_voller_model or cs_solidification_set_voller_model_no_velocity in a more specific situation).

Advanced usage

To access more settings, it is possible to retrieve the structure managing the voller model and to specify advanced parameter settings in order to set the non-linear iterative algorithm for instance.

  {
    cs_solidification_voller_t
      *model_struct = cs_solidification_get_voller_struct();
 
    /* Drive the convergence of the non-linear algorithm to update the thermal
     * source term. */
 
    model_struct->nl_algo->cvg_param.n_max_iter = 20;
    model_struct->nl_algo->cvg_param.rtol = 1e-3; /* relative tolerance */
  }

Binary alloy model

The main function to set a binary alloy model is cs_solidification_set_binary_alloy_model (follow the link to get a description of the parameters). This function is mandatory and has to be located in cs_user_model after calling cs_solidification_activate

Parameters 1 and 2 correspond to the name of the equation related to the solute transport and the name of the unknow associated to this equation (this will be the name of the variable field).
Parameters 3 to 6 correspond to the settings of the Boussinesq term (two contributions: the classical thermal one given by a reference temperature and a thermal dilation coefficient in 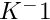; the solutal contribution to the Boussinesq term given by a reference concentration and a solutal dilation coefficient)
Parameters 7 to 10 correspond to the main parameters describing the phase diagram (the partition coefficient between solid and liquid phase, the liquidus slope, the eutectic temperature and the melting temperature for a pure material which corresponds to the one obtained when one of the component of the binary alloy is not present).
Parameter 11 is the value of the diffusivity for the solute transport equation
Parameters 12 and 13 correspond to the latent heat of the alloy (assumed to be constant) and the secondary dendrite arm spacing (a model parameter taking into account micro-segregation phenomena).

  {
    /* Physical data for the settings a binay alloy model */
 
    cs_real_t  T0 = 0.5, beta_t = 0.01;
    cs_real_t  conc0 = 1.0, beta_c = 0.01;
    cs_real_t  ml = -0.1, kp = 0.1;
    cs_real_t  t_eutec = -0.1, t_melt = 0.2;
    cs_real_t  diff_val = 0;
    cs_real_t  latent_heat = 5;
    cs_real_t  s_das = 0.33541;
 
    /* Set the parameters for the binary alloy model */
 
    cs_solidification_set_binary_alloy_model("C_solute",
                                             "C_bulk",
                                             /* Boussinesq approximation */
                                             beta_t,
                                             T0,
                                             beta_c,
                                             conc0,
                                             /* Phase diagram */
                                             kp,
                                             ml,
                                             t_eutec,
                                             t_melt,
                                             /* Solute transport equation */
                                             diff_val,
                                             /* Physical constants */
                                             latent_heat,
                                             s_das);
 
  }

Advanced usage

To access more settings, it is possible to retrieve the structure managing the binary alloy model and to specify advanced parameter settings.

  {
    cs_solidification_binary_alloy_t
      *model_struct = cs_solidification_get_binary_alloy_struct();
 
    int  n_iter_max = 10;
    double  delta_eps = 1e-3;
 
    /* Drive the convergence of the coupled system (solute transport and thermal
     * equation) with respect to the following criteria (taken from Voller and
     * Swaminathan'91)
     *   max_{c\in C} |Temp^(k+1) - Temp^(k)| < delta_tolerance
     *   max_{c\in C} |Cbulk^(k+1) - Cbulk*^(k)| < delta_tolerance
     *   n_iter < n_iter_max
     */
 
    model_struct->n_iter_max = n_iter_max;
    model_struct->delta_tolerance = delta_eps;
  }

Property settings

The creation of all properties used the solidification model is made automatically. The definition is then performed in the function cs_user_finalize_setup

In simple cases, the main properties are constant (uniform and steady-state) and the definition is thus simply done in the example below. Please notice that predefined properties have a macro to store their name. Here are used:

CS_PROPERTY_MASS_DENSITY for the (volumetric) mass density which corresponds to the property named "mass_density" (this is different from the legacy Finite Volume where "density" is used);
CS_NAVSTO_LAM_VISCOSITY for the laminar (dynamic) viscosity which corresponds to the property named "laminar_viscosity";
CS_THERMAL_CP_NAME for the thermal capacity which corresponds to the property named "thermal_capacity";
CS_THERMAL_LAMBDA_NAME for the thermal conductivity which corresponds to the property named "thermal_conductivity".

  {
    /* All the following properties are isotropic and set on all the mesh cells
       (this implies NULL for the second argument). If the property is
       piecewise constant, then replace NULL by the name of a volum zone. */
 
    /* Mass density (kg.m^-3) */
 
    cs_property_t  *rho = cs_property_by_name(CS_PROPERTY_MASS_DENSITY);
    cs_real_t  rho0 = 1;
    cs_property_def_iso_by_value(rho, NULL, rho0);
 
    /* Laminar dynamic viscosity (Pa.s) */
 
    cs_property_t  *mu = cs_property_by_name(CS_NAVSTO_LAM_VISCOSITY);
    cs_real_t  mu0 = 1;
    cs_property_def_iso_by_value(mu, NULL, mu0);
 
    /* Thermal heat capacity */
 
    cs_property_t  *cp = cs_property_by_name(CS_THERMAL_CP_NAME);
    cs_real_t  cp0 = 1.;
    cs_property_def_iso_by_value(cp, NULL, cp0);
 
    /* Thermal conductivity */
 
    cs_property_t  *lambda = cs_property_by_name(CS_THERMAL_LAMBDA_NAME);
    cs_real_t  lambda0 = 0.001;
    cs_property_def_iso_by_value(lambda, NULL, lambda0);
  }

Equation settings

The last step is to set the initial condition and the boundary conditions. By default, all variable fields are set to zero. For the boundary conditions, if nothing is set, then the default boundary condition is applied. For the thermal equation, the default boundary condition is a no flux (i.e. a homogeneous Neumann boundary condition).

  {
    cs_real_t  t_ref = 0.5;
 
    cs_equation_param_t  *th_eqp = cs_equation_param_by_name(CS_THERMAL_EQNAME);
 
    /* Set the initial value for the temperature */
 
    cs_equation_add_ic_by_value(th_eqp, NULL, &t_ref);
 
    /* Set the value of the boundary conditions.
     *
     * The other boundary zones are associated to the default boundary (by
     * default, the thermal equation is associated to a no flux (Homogeneous
     * Neumann boundary condition) */
 
    cs_real_t  Th = t_ref, Tc = -t_ref;
    cs_equation_add_bc_by_value(th_eqp, CS_PARAM_BC_DIRICHLET, "left", &Tc);
    cs_equation_add_bc_by_value(th_eqp, CS_PARAM_BC_DIRICHLET, "right", &Th);
  }

When a solute transport equation is added (this done automatically when calling the function cs_solidification_set_binary_alloy_model), the default boundary condition for this equation is a no flux condition as well.

Here is an example how to set the initial solute concentration in the domain.

  {
    cs_real_t  c_ref = 0.5;
 
    /* One assumes that an equation called "C_solute" has been added */
 
    cs_equation_param_t  *c_eqp = cs_equation_param_by_name("C_solute");
 
    /* Set the initial value for the solute concentration to the reference
       value */
 
    cs_equation_add_ic_by_value(c_eqp, NULL, &c_ref);
 
  }

For the Navier-Stokes equation, the default boundary condition is defined when the domain boundaries are defined in the function cs_user_model using the function cs_boundary_set_default There are two possibilities: