Set inlet boundary condition values for turbulence variables based on a diameter 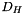 and the reference velocity
and the reference velocity 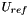 for a circular duct flow with smooth wall.
More...
for a circular duct flow with smooth wall.
More...
 Collaboration diagram for turbulence_bc_inlet_hyd_diam:
Collaboration diagram for turbulence_bc_inlet_hyd_diam:Public Member Functions | |
| subroutine | turbulence_bc_inlet_hyd_diam (face_num, uref2, dh, rho, mu, rcodcl) |
Set inlet boundary condition values for turbulence variables based on a diameter 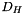 and the reference velocity
and the reference velocity 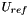 for a circular duct flow with smooth wall.
for a circular duct flow with smooth wall.
We use the laws from Idel'Cik, i.e. the head loss coefficient 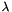 is defined by:
is defined by:
![\[ |\dfrac{\Delta P}{\Delta x}| = \dfrac{\lambda}{D_H} \frac{1}{2} \rho U_{ref}^2 \]](form_109.png)
then the relation reads 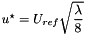 .
. 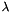 depends on the hydraulic Reynolds number
depends on the hydraulic Reynolds number 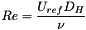 and is given by:
and is given by:
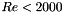
![\[ \lambda = \dfrac{64}{Re} \]](form_114.png)
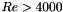
![\[ \lambda = \dfrac{1}{( 1.8 \log_{10}(Re)-1.64 )^2} \]](form_116.png)
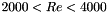 , we complete by a straight line
, we complete by a straight line
![\[ \lambda = 0.021377 + 5.3115. 10^{-6} Re \]](form_118.png)
From 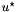 , we can estimate
, we can estimate 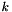 and
and 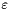 from the well known formulae of developped turbulence
from the well known formulae of developped turbulence
![\[ k = \dfrac{u^{\star 2}}{\sqrt{C_\mu}} \]](form_120.png)
![\[ \varepsilon = \dfrac{ u^{\star 3}}{(\kappa D_H /10)} \]](form_121.png)
| [in] | face_num | boundary face number |
| [in] | uref2 | square of the reference flow velocity |
| [in] | dh | hydraulic diameter 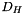 |
| [in] | rho | mass density 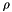 |
| [in] | mu | dynamic viscosity 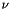 |
| [out] | rcodcl | boundary condition values |
| subroutine turbulence_bc_inlet_hyd_diam | ( | integer(c_int), value | face_num, |
| real(c_double), value | uref2, | ||
| real(c_double), value | dh, | ||
| real(c_double), value | rho, | ||
| real(c_double), value | mu, | ||
| real(kind=c_double), dimension(*) | rcodcl | ||
| ) |