7.1
general documentation
Examples of data settings for volume mass injection

Injection of mass directly in the volume (based on mass source terms) can be defined for selected volume zones. Appropriate zones may be defined in the usual manner, using the GUI, or in the cs_user_zones user-defined function (see examples).

The equation for mass conservation becomes: 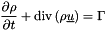$ \der{\rho}{t}+\divs{(\rho \vect{u})}=\Gamma $

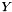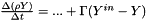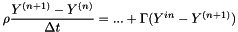
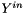The equation for a variable $ \varia $ becomes: $ \frac{\Delta(\rho\varia)}{\Delta t} = ... + \Gamma(\varia^{in} - \varia) $ discretized as $ \rho \dfrac{\varia^{(n+1)} - \varia^{(n)}}{\Delta t} = ... + \Gamma(\varia^{in} - \varia^{(n+1)}) $

$ \varia^{in} $ is the value of 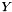$ \varia $ associated to the injected mass.

Two options are available:

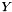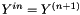  • the mass flux is injected with the local value of variable $ \varia $: $ \varia^{in} = \varia^{(n+1)} $ (the equation for 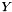$ \varia $ is therefore not modified, and no value needs to be assigned)
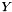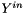  • the mass flux is injected with a specific value for $ \varia $: $ \varia^{in} $ is specified by the user

Variables to be specified by the user

Remarks
  • if no value is specified for a given variable, the local value is used in that zone.
  • if the specified mass source term value is < 0, mass is removed from the system, therefore code_saturne automatically considers 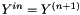$ \varia^{in}=\varia^{(n+1)}$ for variables other than pressure, whatever the values of itypsm or smacel specified by the user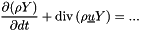
  • if a scalar doesn't evolve following the standard equation $ \dfrac{\partial{(\rho \varia)}}{\partial{dt}} + \divs{(\rho \vect{u} \varia)} = ...$ (alternate convective field for instance), the source term set by this routine will not be correct (except in case of injection at the local value of the variable). The proper source term should be added directly in cs_user_source_terms.

Simulation of an inlet condition by mass source terms

When using constant values per zone, an inlet condition can easily be defined adding code similar to the following snipped in the cs_user_finalize_setup function (in cs_user_parameters.c):

cs_real_t wind = 0.1;
cs_real_t dh = 0.5;
const char z_name[] = "mass_injection";
/* Pressure */
double mass_in[1] = {30000};
cs_equation_add_volume_mass_injection_by_value
(cs_field_get_equation_param(CS_F_(p)), z_name, mass_in);
/* Velocity */
double vel_in[3] = {0, wind, 0};
cs_equation_add_volume_mass_injection_by_value
(cs_field_get_equation_param(CS_F_(vel)), z_name, vel_in);
/* Turbulence values */
cs_turbulence_inflow_volume_mass_injection_ke_hyd_diam
(z_name,
cs_math_sq(wind),
dh,
cs_glob_fluid_properties->ro0,
cs_glob_fluid_properties->viscl0);
/* Scalars */
int n_fields = cs_field_n_fields();
for (int f_id = 0; f_id < n_fields; f_id++) {
cs_field_t *f = cs_field_by_id(f_id);
int scalar_id = (f->type & CS_FIELD_VARIABLE) ?
cs_field_get_key_int(f, cs_field_key_id("scalar_id")) : -1;
if (scalar_id >= 0) {
double val = 1;
cs_equation_add_volume_mass_injection_by_value
(cs_field_get_equation_param(f), z_name, &val);
}
}

The value assigned to the pressure is the mass injection rate. For other variables, it is the injected value itself. Note that turbulence variable values based on a hydraulic diameter can and reference velocity easily be set using the function cs_turbulence_inflow_volume_mass_injection_ke_hyd_diam.

Advanced definitions

It is also possible to define more complex injection mass flows using an analytical function. This first requires defining a function matching the cs_analytic_func_t template, such as the one below:

static void
_define_injection(cs_real_t time,
cs_lnum_t n_elts,
const cs_lnum_t *elt_ids,
const cs_real_t *xyz,
bool dense_output,
void *input,
cs_real_t *res)
{
CS_UNUSED(time);
CS_UNUSED(xyz);
cs_field_t *f = input; /* Current field for which this injection is called */
const cs_zone_t *z = cs_volume_zone_by_name("mass_injection");
/* Injection mass flow rate */
cs_real_t xgamma = 30000;
if (z->measure <= 0)
bft_error(__FILE__, __LINE__, 0,
"In function %s: volume of zone %d (%s) is %g.",
__func__, z->id, z->name, z->measure);
/* Assume output directly to main arrays, so not handle dense case */
if (dense_output == false)
bft_error(__FILE__, __LINE__, 0,
"Function %s currently only handles dense output.",
__func__);
/* For pressure
------------ */
if (f == CS_F_(p)) {
const cs_mesh_quantities_t *mq = cs_glob_mesh_quantities;
const cs_real_t *cell_f_vol = mq->cell_f_vol;
for (cs_lnum_t i = 0; i < n_elts; i++) {
res[i] = xgamma;
}
/* Logging: compute/check the mass flow rate in the volume */
static bool _logged_mass_flux = false;
if (_logged_mass_flux == false && cs_log_default_is_active()) {
const cs_equation_param_t *eqp = cs_field_get_equation_param(f);
if (eqp->verbosity >= 1 || _logged_mass_flux == false) {
cs_real_t flucel = 0.;
for (cs_lnum_t i = 0; i < n_elts; i++) {
cs_lnum_t c_id = elt_ids[i];
flucel += cell_f_vol[c_id] * res[i];
}
cs_parall_sum(1, CS_REAL_TYPE, &flucel);
cs_log_printf(CS_LOG_DEFAULT,
(" Mass rate generated in the domain: %14.5e\n"
" ----------------------------------\n"),
flucel);
_logged_mass_flux = true;
}
}
}
}

Note that this function injects mass uniformly, but also computes and logs the mass rate generated in the domain.

To use this function for a given volume injection, we define the injection as follows:

cs_field_t *f = CS_F_(p);
cs_equation_add_volume_mass_injection_by_analytic
(cs_field_get_equation_param(f),
z_name,
_define_injection, // associated function
f); // input structure (use field to access info)

In this example, we have assigned the field pointer to the function input, so the function can query the field used for a given call, and could be adapted to handle different variables (which avoids requiring a different function for each variable).

Note that in an actual application, the mass balance can be checked using the balance_by_zone_compute or balance_by_zone_compute functions, so using a more complex injection function is useful only when trying to replicate the mass source terms user function behavior used in previous versions of code_saturne.

Simulation of suction by a pump

In the following example, we simulate the suction (by a pump for instance) with a total rate of 80 000 kg/s. The suction rate is supposed to be uniformly distributed on all the cells in the "suction_pump" zone.

double mass_out[1] = {-80000};
cs_equation_add_volume_mass_injection_by_qov
(cs_field_get_equation_param(CS_F_(p)), "suction_pump", mass_out);

As mass is removed, there is no need to define the values for variables other than pressure. Using cs_equation_add_volume_mass_injection_by_qov, ("quantity over a volume"), the prescribed value is automatically distributed over the associated zone.