Source terms for transported scalars may be defined using the cs_user_source_terms user-defined function.
The following initialization block or portions thereof needs to be added for the following examples:
Indicator of variance scalars: To determine whether a scalar is a variance, the following info can be accessed:
var_f_id == -1 , the scalar is not a variance var_f_id >= 0 , the field is the variance of the scalar with field id var_f_id Density
Example of arbitrary source term for the scalar f, named "scalar_2" in the calculation.
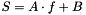
appearing in the equation under the form
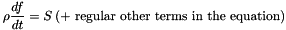 In the following example:
In the following example:
![\[A=-\frac{\rho}{\tau_f} \]](form_797.png)
![\[B=\rho \cdot prod_f \]](form_798.png)
with:
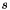 ) (dissipation time for
) (dissipation time for 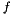 )
)![$ [f]\cdot s^{-1} $](form_800.png) ) (production of
) (production of 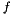 by unit of time)
by unit of time)which yields:
st_imp[i] = volume[i]*A = -volume[i]*rho/tauf st_exp[i] = volume[i]*B = volume[i]*rho*prod_f Source term applied to second scalar
Example of arbitrary volumic heat term in the equation for enthalpy h.
In the considered example, a uniform volumic source of heating is imposed in the cells with coordinate X in [0;1.2] and Y in [3.1;4].
The global heating power if Pwatt (in 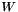 ) and the total volume of the selected cells is
) and the total volume of the selected cells is volf (in 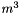 ).
).
This yields:
st_imp[i] = 0 st_exp[i] = volume[i]* pwatt/volf 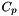 because
because 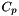 is put outside the diffusion term and multiplied in the temperature equation as follows:
is put outside the diffusion term and multiplied in the temperature equation as follows:
![\[ \rho C_p \norm{\vol{\celli}} \frac{dT}{dt} + ... = \norm{\vol{\celli}[i]} \frac{pwatt}{voltf} \]](form_803.png)
with pwatt = 100.0