7.1
general documentation
Functions/Subroutines
atmcls.f90 File Reference

Compute friction velocity u* and surface sensible heat flux q0 for a non neutral atmospheric surface layer using the explicit formula developed for the ECMWF by Louis (1982) More...

Functions/Subroutines

subroutine atmcls (ifac, utau, rough_d, duplus, dtplus, yplus_t, uet, gredu, cfnns, cfnnk, cfnne, dlmo, temp, totwt, liqwt, icodcl, rcodcl)
 

Detailed Description

Compute friction velocity u* and surface sensible heat flux q0 for a non neutral atmospheric surface layer using the explicit formula developed for the ECMWF by Louis (1982)

Function/Subroutine Documentation

◆ atmcls()

subroutine atmcls ( integer  ifac,
double precision  utau,
double precision  rough_d,
double precision  duplus,
double precision  dtplus,
double precision  yplus_t,
double precision  uet,
double precision  gredu,
double precision  cfnns,
double precision  cfnnk,
double precision  cfnne,
double precision  dlmo,
double precision  temp,
double precision  totwt,
double precision  liqwt,
integer, dimension(nfabor,nvar)  icodcl,
double precision, dimension(nfabor,nvar,3)  rcodcl 
)
Parameters
[in]ifactreated boundary face
[in]utautangential mean velocity
[in]rough_droughness z0
[in]duplus1 over dimensionless velocity in neutral conditions
[in]dtplus1 over dimensionless temperature in neutral conditions
[in]yplus_tthermal dimensionless wall distance
[out]uetfriction velocity
[out]gredureduced gravity for non horizontal wall
[out]cfnnsnon neutral correction coefficients for profiles of scalar
[out]cfnnknon neutral correction coefficients for profiles of k
[out]cfnnenon neutral correction coefficients for profiles of eps
[out]dlmoinverse Monin Obukhov length (for log only)
[in]temppotential temperature in boundary cell
[in]totwttotal water content in boundary cell
[in]liqwtliquid water content in boundary cell
[in]icodclface boundary condition code:
  • 1 Dirichlet
  • 2 Radiative outlet
  • 3 Neumann
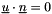
  • 4 sliding and $ \vect{u} \cdot \vect{n} = 0 $
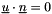
  • 5 smooth wall and $ \vect{u} \cdot \vect{n} = 0 $
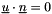
  • 6 rough wall and $ \vect{u} \cdot \vect{n} = 0 $
  • 9 free inlet/outlet (input mass flux blocked to 0)
  • 11 Boundary value related to the next cell value by an affine function
  • 13 Dirichlet for the advection operator and Neumann for the diffusion operator
[in]rcodclboundary condition values:
  • rcodcl(1) value of the dirichlet
  • rcodcl(2) value of the exterior exchange coefficient (infinite if no exchange)
  • rcodcl(3) value flux density (negative if gain) in w/m2
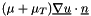
    1. for the velocity $ (\mu+\mu_T) \gradv \vect{u} \cdot \vect{n} $
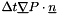
    2. for the pressure $ \Delta t \grad P \cdot \vect{n} $
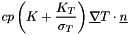
    3. for a scalar $ cp \left( K + \dfrac{K_T}{\sigma_T} \right) \grad T \cdot \vect{n} $