code_saturne User's Forum

Posted: **Wed Aug 20, 2025 5:29 pm**

Hello everyone,

I have a question about the scalar diffusion coefficient set in the GUI under:
Volume conditions > all_cells > Diffusion coefficient of species.

For a bit of context i am talking about an atmospheric simulation where i define a user scalar to transport with the SGDH flux model (since i am using a k-epsilon turbulence model).

According to the theory guide p.18, the genearl scalar transport equation is :
$\frac{\partial (\rho a)}{\partial t} + {\nabla \cdot (\rho a \mathbf{u})} - {\nabla \cdot (K \nabla a)} = S_{T_a} + \Gamma a_{\text{in}} \label{eq:scalar_transport}$

And the SGDH detail p.80 gives :
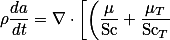$\rho \frac{da}{dt} = \nabla \cdot \left[ \left( \frac{\mu}{\text{Sc}} + \frac{\mu_T}{\text{Sc}_T} \right) \nabla a \right] \label{eq:gradient_diffusion}$

I arrived to the conclusion that the general formula for a scalar transport with the SGDH model is (and correct me if i'm wrong) :
$\frac{\partial (\rho a)}{\partial t} + \nabla \cdot (\rho a \mathbf{u}) - \nabla \cdot \left( \left( \frac{\mu}{\text{Sc}} + \frac{\mu_T}{\text{Sc}_T} \right) \nabla a \right) = S_{T_a} + \Gamma a_{\text{in}} \label{eq:full_scalar_transport}$

But at this point i'm not sure where the scalar difusion coefficient is used. My best guess would be that it defines the $\frac{\mu}{\text{Sc}}$ part of the equation (the molecular diffusion part) with the following relation : $D =\frac{\mu}{\rho . \text{Sc}}$ .
And i also assume the turbulent part $\frac{\mu_T}{\text{Sc}_T}$ is handled automatically by the SGDH model using μT from the k-ε model

Am i guessing wrong or not ? Thanks for your help.

Regards,

Cyril

code_saturne User's Forum

Diffusion coefficient of species in SGDH

Diffusion coefficient of species in SGDH