Question about the convergence of LES calculations 2

[wangyw]

Hello everyone,

A few months ago, I posted a question on the forum regarding the failure of my LES (Smagorinsky or WALE) numerical simulation to converge. The link to the original post is viewtopic.php?t=3277.

Recently, in order to better identify the reason of my numerical divergence, I conducted calculations using a relatively simpler model, i.e. the NACA0012 airfoil. The version I used is v8.0.3. Here are some main simulation parameters.

• 1. Computation Domain and Mesh: A qusi-three-dimensional numerical simulation of airfoil flow was conducted using a rectangular computational domain. A two-dimensional computational mesh was first generated, in which quadrilateral elements were used within the boundary layer around the airfoil surface, and triangular elements were used in the far-field region. Subsequently, this 2-D mesh was extruded along the spanwise direction by 3 grid points to create a three-dimensional hybrid mesh for the quasi-3D simulation As a result, the mesh on the airfoil surface consists of hexahedra, and the mesh in the far-field region consists of pentahedra (triangular prisms).

• 2. Boundary Conditions: The streamwise direction was configured with a velocity inlet and a pressure outlet, while both the spanwise and cross-stream directions employed periodic boundary conditions

.

• 3. Simulation Parameters: In LES simulation, I ensured that the time step keeps the maximum value of Courant number always below 1.0. Besides, the wall y+ of my mesh is around 1.0, and the Reynold Numbers I tried are 50000 and 500000. The blending factor in the scheme of velocity equation is set to 0.98.

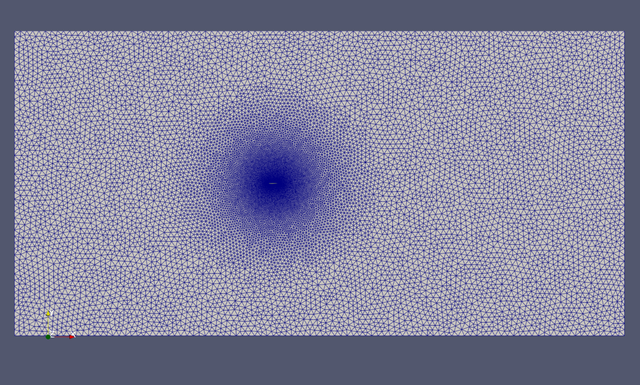
Figure 1 Rectangular computational domain and hybrid mesh


Figure 2 Hybrid mesh around the airfoil surface.

Consistent with the problem described in my inquiry several months ago, the RANS simulation for the NACA0012 airfoil converges and produces physically meaningful results. However, the LES simulation fails to achieve convergence. The specific manifestations are as follows:

• 1. If I use the converged solution obtained from the RANS simulation as the initial field for the LES calculation, some anomalous velocity points appear in the far-field region at the first step of the LES computation. These anomalies fail to dissipate as the simulation progresses. Additionally, similar velocity abnormalities are observed in the unstructured (pentahedral) mesh region near the airfoil.

Figure 3 Streamwise velocity contour (full computation domain) of the 2000th time-step in LES simulation with RANS results as initial condition


Figure 4 Streamwise velocity contour (near airfoil surface) of the 2000th time-step in LES simulation with RANS results as initial condition

• 2. If a uniform velocity field is used as the initial condition, velocity anomalies also arise in the unstructured (pentahedral) mesh region near the airfoil, ultimately leading to failure in achieving convergence.

Figure 5 Streamwise velocity contour (near airfoil surface) of the 2000th time-step in LES simulation with uniform velocity field as initial condition

Could you please kindly give me some advice on how to improve the convergence of LES (WALE of Smagorinsky) simulations?

Thank you very much in advance and best regards,
WangYW

[Yvan Fournier]

Hello,

As I mentioned in the previous topic, code_saturne can be very sensitive to the mesh quality in LES computations, and there is no simple way to solve this, except to use a more regular (ideally hexa-blocked) mesh, and avoid abrubt changes in refinement.

Some numerical options, such as the number of sweeps or gradient reconstruction options (such as using an extended neighborhood) can help. Using SOLU type algorithms is often more stable than the default centered algorithm, but any upwind algorithm tends to lead to loss of energy conservation, which is an issue for LES simulation quality.

Again, the mesh regularity is more importent than just the cell type. We tested splitting tetrahedra into 8 hexahedra with an intern last year, and results were no better than with a tetrahedral mesh. So spending a bit more time on the mesh to replace triangular prisms with hexahedra can pay off in terms of results quality and speed of convergence, though depending on the geometry, it is not always easy. Note that though using non-conformal mesh interfaces can also degrade LES computations, its effects might not ba as bad as having prism elements whose triangular sides are parallel to the flow (i.e. amounting to triangles in 2D), so in a geometry with many constraints, it might be an alternative worth trying.

Best regards,

Yvan