Parallelism and periodicity

Parallelism basics

Parallelism is based on domain partitioning: each processor is assigned a part of the domain, and data for cells on parallel boundaries is duplicated on neighboring processors in corresponding "ghost", or "halo" cells (both terms are used interchangeably). Values in these cells may be accessed just the same as values in regular cells. Communication is only required when cell values are modified using values from neighboring cells, as the values in the "halo" can not be computed correctly (since the halo does not have access to all its neighbors), so halo values must be updated by copying values from the corresponding cells on the neighboring processor.

Compared to other tools using a similar system, a specificity of code_saturne is the separation of the halo in two parts: a standard part, containing cells shared through faces on parallel boundaries, and an extended part, containing cells shared through vertices, which is used mainly for least squares gradient reconstruction using an extended neighborhood. Most updates need only to operate on the standard halo, requiring less data communication than those on the extended halos.

Parallel domain partitioning: halos

Periodicity

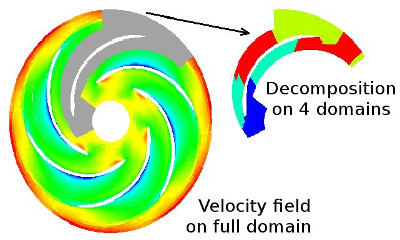
Periodicity is handled using the same halo structures as parallelism, with an additional treatment for vector and coordinate values: updating coordinates requires applying the periodic transformation to the copied values, and in the case of rotation, updating vector and tensor values also requires applying the rotation transformation. Ghost cells may be parallel, periodic, or both. The example of a pump combining parallelism and periodicity is given in the following figure In this example, all periodic boundaries match with boundaries on the same domain, so halos are either parallel or periodic.

Combined parallelism and periodicity: halos

Coding operations in parallel mode

In parallel mode, the user must pay attention when performing global operations. The following list is not exhaustive:

• calculation of extreme values on the domain (for instance, minimum and maximum of some calculation values);
• test of the existence of a certain value (for instance, do faces in a certain group exist?);
• verification of a condition on the domain (for instance, is a given flow value reached somewhere?);
• counting out of entities (for instance, how many cells have a nonzero source term value ?);
• global sum (for instance, calculation of a mass flow or the total mass of a pollutant).
• Access to values in neighboring cells: with periodicity or parallelism, some interior faces will be on parallel boundaries. When values in these cells may have been modified locally, it is necessary to "synchronize" the ghost values for that array, using functions such as cs_halo_sync_var, before using the face neighbor values.
• The cs_glob_rank_id and cs_glob_n_ranks global variables can be used to query the current rank id (-1 in serial model, 0 to n-1 in parallel) and the number of ranks.
• The presence of periodicity is tested with the variable cs_glob_mesh->n_init_perio (> 1 if periodicity is activated);
  • The presence of rotation periodicity is tested with the cs_glob_mesh->have_rotation_perio variable.

The user may refer to the different parallel operation examples present.

Care should be taken with the fact that the boundaries between subdomains consist of internal faces shared between two processors (these are indeed internal faces, even if they are located at a "processor boundary". They should not be counted twice (once per processor) during global operations using internal faces (for instance, counting the internal faces per processor and summing all the obtained numbers drives into over-evaluating the number of internal faces of the initial mesh).

Logging operations in parallel mode

When running in parallel, only the first rank actually produces outputs when writing to run_solver.log using the cs_log_printf function.

This avoids requiring tests in calling code, which would add clutter an could easily be forgotten.

File ouptut operations in parallel mode

When writing simple output to files, it is important to check for the local rank, and to avoid writing to a same file from multiple processors, unless dedicated features are used, such as the cs_file.c functions.

Some notes about periodicity

Note that periodic faces are not part of the domain boundary: periodicity is interpreted as a "geometric" condition rather than a classical boundary condition.

Some particular points should be noted:

• Periodicity should work when the periodic boundaries are meshed differently (periodicity of non-conforming faces), except for the case of a 180 degree rotation periodicity.
• Rotation periodicity is incompatible with
  • semi-transparent radiation,
  • reinforced velocity-pressure coupling ipucou=1