Injection of mass directly in the volume (based on mass source terms) can be defined for selected volume zones. The mass conservation equation is then modified as follows:

$\frac{\partial \rho}{\partial t} + div(\rho\vect{u})=\Gamma$

Γ is the mass source term expressed in kg.m^-3.s^-1.

The presence of a mass source term modifies the evolution equation of the other variables, too. Let 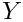$\varia$ be any solved variable apart from the pressure (velocity component, turbulent energy, dissipation, scalar, ...). Its evolution equation becomes:

$\frac{\Delta(\rho\varia)}{\Delta t} = ... + \Gamma(\varia^{in} - \varia)$

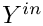
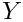
$\varia^{in}$ is the value of $\varia$ associated to the mass entering or leaving the domain. After discretization, the equation may be written:

$\rho \dfrac{\varia^{(n+1)} - \varia^{(n)}}{\Delta t} = ... + \Gamma(\varia^{in} - \varia^{(n+1)})$

Mass source terms can be defined using the cs_equation_add_volume_mass_injection series of functions in cs_user_finalize_setup. The value assigned to the pressure variable is the mass injection rate.

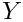
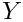
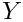
For each other variable $\varia$ , there are two possibilities:

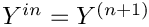
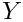
We can consider that the mass is added (or removed) with the ambient value of $\varia$ . In this case $\varia$ : $\varia^{in} = \varia^{(n+1)}$ and the equation of $\varia$ is not modified (so no specific definition needs to be added).
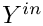
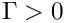
Or we can consider that the mass is added with an imposed value $\varia^{in}$ (this solution is physically correct only when the mass is effectively added, $\Gamma > 0$ ).

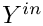
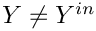
For the variance, do not take into account the scalar $\varia^{in}$ in the environment where $\varia \ne \varia^{in}$ generates a variance source.

Examples of data settings for volume mass injection

Further details and examples in the linked example page above.