Introduction

Two classical models are available in code_saturne for rotor/stator interactions modelling in turbomachinery computations: the steady approach which is based on the so-called Frozen Rotor modelling and the transient rotor/stator approach which is based on a sliding mesh technique.

Warning

This section describes these functionalities based on a single code_saturne computation. An alternative rotor/stator coupling based on coupling of boundary conditions is also possible (and only briefly described in this section) but it is not recommended.

Meshing recommendations

Periodicity

The rotational periodicity treatment is possible only in Frozen Rotor. However, the interface plane between rotor and stator must match in the azimutal $\theta$ direction:

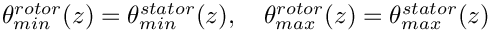
$\theta_{min}^{rotor}(z)=\theta_{min}^{stator}(z),\quad\theta_{max}^{rotor}(z)=\theta_{max}^{stator}(z)$

for all 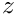through the rotation axis direction.

Rotor/stator interface

Unsteady rotor/stator: in the input mesh(es), the interface between rotor and stator domains has to be composed of \underline boundary faces. Then the interface boundary faces are joined during the computation and become internal faces, as is usual for mesh joining in the preprocessing stage. A simple way to ensure joining is not done prematurely is to provide \underline separated meshes for each rotor or stator domain.

Frozen Rotor: the interface can be composed of boundary faces (in which case the interface boundary faces are joined at the beginning of the computation) or of internal faces.

Meshing of the interface region

As mentioned above, when a rotor/stator interface boundary exists (in particular for the unsteady rotor/stator model), boundary faces are joined by the solver during the computation, based on the current rotor position. It is thus important to be aware that the success of a joining operation is strongly dependant on the \underline quality of the mesh at the interface. More precisely, the refinement must be as similar as possible at both sides of the interface. Moreover, it is reminded that the tolerance parameter of a joining is a fraction of the shortest edge linked with a vertex of a joined face. Consequently, cells with high aspect ratios where the refinement in the azimutal $\theta$ direction is much coarser than those in one of the two others can also lead to a joining failure. In particular, the user should be careful to avoid elongated viscous layer type cells in curved areas such as a rotor-stator interface.

If the meshes at both sides of the interface are very different such that the joining fails, advanced joining parameters are available. However, modifying the mesh is more likely to succeed. The introduction of a somekind of buffer cells layer on both sides of the interface should be very valuable. Ideally, each of the two layers should have the same refinement and a constant azimutal step (this latter recommandation is relevant only for unsteady rotor/stator model).

Alternative rotor/stator coupling

If the meshes at both sides of the interface are very different and can not be modified, a fallback solution is to use the rotor/stator model based on the boundary conditions coupling.

\Warning: Contrarily to the mesh joining approach, the boundary conditions coupling approach is not fully conservative.

Turbomachinery dedicated postprocessing functions

Useful postprocessing functions relative to the machinery characteristics are available: postprocessing of the couple on the rotor walls and postprocessing of the head generated by the machinery.

Data setting, keywords and examples

Data setting, keywords and examples for turbomachinery computations (mesh joining or boundary conditions coupling), are provided in the dedicated doxygen documentation.