Additional right-hand side source terms for velocity components equation (Navier-Stokes)

Usage

The additional source term is decomposed into an explicit part 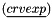$(\vect{crvexp})$ and an implicit part 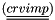$(\tens{crvimp})$ that must be provided here. The resulting equation solved by the code for a velocity is:

$\rho \norm{\vol{\celli}} \DP{\vect{u}} + .... = \tens{crvimp}\cdot \vect{u} + \vect{crvexp}$

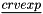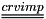Note that $\vect{crvexp}$ and $\tens{crvimp}$ are defined after the Finite Volume integration over the cells, so they include the 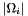$\norm{\vol{\celli}}$ term. More precisely:

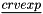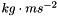
$\vect{crvexp}$ is expressed in $kg\cdot ms^{-2}$
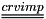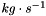
$\tens{crvimp}$ is expressed in $kg\cdot s^{-1}$

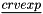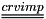The $\vect{crvexp}$ and $\tens{crvimp}$ arrays are already initialized to 0 before entering the the routine. It is not needed to do it in the routine (waste of CPU time).

For stability reasons, Code_Saturne will not add -crvimp directly to the diagonal of the matrix, but Max(-crvimp,0). This way, the 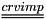$\tens{crvimp}$ term is treated implicitely only if it strengthens the diagonal of the matrix. However, when using the second-order in time scheme, this limitation cannot be done anymore and -crvimp is added directly. The user should therefore test the negativity of crvimp by himself.

When using the second-order in time scheme, one should supply:

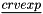$\vect{crvexp}$ at time n
$\tens{crvimp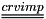}$ at time n+1/2

The selection of cells where to apply the source terms is based on a getcel command. For more info on the syntax of the getcel command, refer to the user manual or to the comments on the similar command getfbr in the routine cs_user_boundary_conditions.

Local variables

! Local variables
character*80     chaine
integer          iel
double precision ckp, qdm, beta
integer, allocatable, dimension(:) :: lstelt
double precision, dimension(:), pointer ::  cvar_temperature
double precision, dimension(:), pointer ::  cpro_rom
type(var_cal_opt) :: vcopt

Initialization and finalization

The following initialization block needs to be added for the following examples:

! Allocate a temporary array for cells selection
allocate(lstelt(ncel))
! --- Get variable calculation options
call field_get_key_struct_var_cal_opt(ivarfl(ivar), vcopt)
if (vcopt%iwarni.ge.1) then
  call field_get_label(ivarfl(ivar), chaine)
  write(nfecra,1000) chaine(1:8)
endif
call field_get_val_s(icrom, cpro_rom)

At the end of the subroutine, it is recommended to deallocate the work array:

! Deallocate the temporary array

deallocate(lstelt)

In theory Fortran 95 deallocates locally-allocated arrays automatically, but deallocating arrays in a symetric manner to their alloacation is good pratice, and avoids using a different logic C and Fortran.

Example

Example of arbitrary source term for component 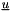$\vect{u}$ :

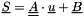$\vect{S} = \tens{A} \cdot \vect{u} + \vect{B}$ appearing in the equation under the form:

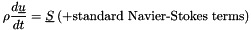
$\rho \dfrac{d\vect{u}}{dt} = \vect{S} \: (+ \text{standard Navier-Stokes terms})$

In the following example:

$\tens{A} = -\rho \cdot \tens{CKP}$

$\vect{B} = \vect{XMMT}$

with:

CKP = 1.d0 (in 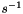$s^{-1}$ ) (return term on velocity)
MMT = 100.d0 (in 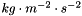$kg \cdot m^{-2} \cdot s^{-2}$ ) (momentum production by volume and time unit)

which yields:

crvimp(1, 1, iel) = volume(iel)* A = - volume(iel)*(rho*CKP )
crvexp(1, iel) = volume(iel)* B = volume(iel)*(XMMT)

Body

ckp  = 10.d0
qdm  = 100.d0
do iel = 1, ncel
  crvimp(1, 1, iel) = - cell_f_vol(iel)*cpro_rom(iel)*ckp
enddo
do iel = 1, ncel
  crvexp(1, iel) = cell_f_vol(iel)*qdm
enddo

Example of a boussinesq momentum source term

Example to add Boussinesq source to the z component of 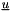$\vect{u}$ :

Body

! Expension coefficient
beta = 1.d0
! Get temperature field
call field_get_val_s_by_name("temperature", cvar_temperature)
do iel = 1, ncel
  crvexp(3, iel) = cell_f_vol(iel) * ro0 * beta * (cvar_temperature(iel) - t0)
enddo