Additional right-hand side source terms for scalar equations (user scalars and specific physics scalars) with ustssc subroutine.

Usage

The routine is called for each scalar, user or specific physisc. It is therefore necessary to test the value of the scalar number iscal to separate the treatments of the different scalars (if (iscal.eq.p) then ....).

The additional source term is decomposed into an explicit part 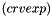$(crvexp)$ and an implicit part 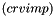$(crvimp)$ that must be provided here. The resulting equation solved by the code for a scalar 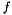$f$ is:

$\rho \norm{\vol{\celli}} \frac{df}{dt} + .... = crvimp \cdot f + crvexp$

Note

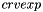and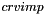

are defined after the Finite Volume integration over the cells, so they include the $\norm{\vol{\celli}}$ term. More precisely: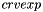

is expressed in $kg\cdot [scal]\cdot s^{-1}$ , where is the unit of the scalar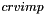
is expressed in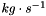 $kg \cdot s^{-1}$

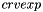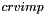The $ crvexp $ and $ crvimp $ arrays are already initialized to 0 before entering the the routine. It is not needed to do it in the routine (waste of CPU time).

For stability reasons, Code_Saturne will not add -crvimp directly to the diagonal of the matrix, but Max(-crvimp,0). This way, the crvimp term is treated implicitely only if it strengthens the diagonal of the matrix. However, when using the second-order in time scheme, this limitation cannot be done anymore and -crvimp is added directly. The user should therefore test the negativity of crvimp by himself.

When using the second-order in time scheme, one should supply:

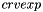at time n
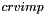at time n+1/2

The selection of cells where to apply the source terms is based on a getcel command. For more info on the syntax of the getcel command, refer to the user manual or to the comments on the similar command getfbr in the routine cs_user_boundary_conditions.

Warning: If scalar is the temperature, the resulting equation solved by the code is:

$\rho C_p \norm{\vol{\celli}} \frac{dT}{dt} + .... = crvimp \cdot T + crvexp$

Note

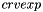and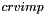

are defined after the Finite Volume integration over the cells, so they include the $\norm{\vol{\celli}}$ term. More precisely: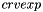

is expressed in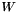
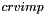is expressed in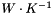 $W \cdot K^{-1}$

Steep source terms

In case of a complex, non-linear source term, say 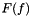$F(f)$ , for scal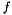ar $f$ , the easiest method is to implement the source term explicitely.

$\frac{df}{dt} = .... + F(f^{(n)})$

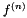where $f^{(n)}$ is the value of 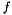$f$ at time 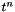$t^n$ , the beginning of the time step.

This yields :

crvexp = volume*F(f(n))
crvimp = 0

However, if the source term is potentially steep, this fully explicit method will probably generate instabilities. It is therefore wiser to partially implicit the term by writing:

$\frac{df}{dt} = .... + \frac{dF}{df} f^{(n+1)} - \frac{dF}{df} f^{(n)} + F(f^{(n)})$

This yields:

crvexp = volume*(F(f(n)) - dF/df*f(n))
crvimp = volume*dF/df

Local variables

! Local variables
integer          iel
double precision, dimension(:,:), pointer :: cvar_vel
double precision ubulk, flux_tot
integer          ifac
double precision ubulkm
data             ubulkm /0.d0/
save             ubulkm

Body

Initialization

ubulk= 0.d0

Map field arrays

call field_get_val_v(ivarfl(iu), cvar_vel)
! Bulk mean velocity (x component)
do iel = 1, ncel
  ubulk = ubulk + cvar_vel(1, iel) * cell_f_vol(iel)
enddo

Parallelism

if (irangp.ge.0) then
  call parsom(ubulk)
endif
ubulk = max(abs(ubulk) / voltot, 1d-12)
! Flux x Total surface / (rho Cp)
flux_tot = 1.d0
do iel = 1, ncel
  crvimp(iel) = 0.d0
  crvexp(iel) = cell_f_vol(iel)*cvar_vel(1, iel) * flux_tot / ubulk
enddo

Formats

1000 format(' User source terms for variable ',a8,/)

End

return

end subroutine ustssc